Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?
Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника
Тема 3. Оптимальный раскрой промышленных материалов
|
|
(лекц. – 2 час., лаб. – 2 час., СРС – 20 час.)
Базовая модель задачи о раскрое соответствует одному виду исходного материала (листов или рулонов), который используется для получения m видов заготовок в заданных объемах bi, i=1,...,m. Предполагается, что выявлено n возможных вариантов раскроя, каждый из которых характеризуется нормами выхода заготовок каждого вида из одного листа (рулона) aij, i=1,..., m, j=1,..., n и площадью листа (рулона), идущей в отход cj, j=1,...,n. Обозначив xj, j=1,...,n - число листов (рулонов), раскраиваемых по j-му варианту, f - суммарную площадь отходов материала, экономико-математическую модель данной задачи запишем в виде:
Найти min f =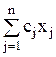 
при условиях
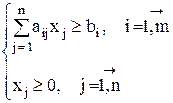
В качестве целевой функции можно использовать суммарное число листов (рулонов), необходимых для раскроя заданного числа заготовок:
f =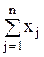 
Основные ограничения могут быть записаны в виде уравнений, однако, в этом случае при неблагоприятном соотношении размеров заготовок, размеров исходного материала и требуемого числа заготовок задача может не иметь решения. С другой стороны, заготовки, выкраиваемые сверх установленного производственного задания, могут рассматриваться как скрытые отходы. Поэтому возможно применение двухсторонних ограничений:
 |
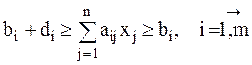где di – допуск на объем i-го заказа.
Основная трудность в решении задачи о раскрое материала состоит в формировании множества допустимых вариантов раскроя, число которых быстро увеличивается с увеличением числа видов заготовок, если применяются “смешанные” варианты раскроя, при которых из листа (рулона) одновременно выкраиваются заготовки разных видов. Применение таких вариантов раскроя обеспечивает наиболее экономное использование исходного материала. Число вариантов “смешанного” раскроя может измеряться десятками, сотнями и тысячами. Поэтому при решении задачи о раскрое необходимо применять персональный компьютер уже на этапе формирования математической модели решаемой задачи.
Рассмотрим алгоритм формирования множества допустимых вариантов раскроя в предположении, что в процессе раскроя лист или рулон разрезается на полосы требуемой ширины, затем каждая полоса режется на отдельные заготовки соответствующего вида. Эта так называемая "гильотинная" схема раскроя наиболее приемлема в технологическом отношении. При этом для каждого вида заготовок может допускаться только долевой раскрой (ширина заготовки ориентируется по ширине исходного материала), только поперечный раскрой (ширина заготовки ориентируется по длине исходного материала) либо и тот и другой вид раскроя.
При описании алгоритма формирования допустимых вариантов раскроя используется понятие “вид полосы”. Вид полосы определяется не только видом заготовок, которые из нее выкраиваются, но и характером раскроя: долевым или поперечным. Таким образом, одному виду заготовок может соответствовать два вида полос, если допускается и долевой и поперечный раскрой заготовок этого вида. Обозначим через k - число видов полос (k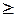 
m). Описываемый ниже алгоритм строится в предположении, что предварительно проведено ранжирование полос в порядке убывания (невозрастания) их ширины. Видом полосы l будем называть ее порядковый номер в списке видов полос после ранжирования (l = 1,..., k).
При гильотинной схеме вариант раскроя характеризуется числом полос каждого вида, вырезаемых из листа или рулона. Первый из допустимых вариантов раскроя формируется “по остаточному принципу”: по ширине листа (рулона) откладывается максимально возможное число полос первого вида (наибольшей ширины), в оставшейся части - второго вида и т.д. до заполнения всей ширины исходного материала. Естественно, что при этом ширина полосы отхода будет меньше ширины последнего вида полос (наименьшей ширины).
От первого и последующих вариантов раскроя будем переходить к очередному варианту по следующему правилу. Если число полос предпоследнего вида в предшествующем варианте не равно нулю, то оно уменьшается на единицу и корректируется (увеличивается) число полос последнего вида - “по остаточному принципу”, число полос остальных видов не меняется по сравнению с предыдущим вариантом раскроя. В противном случае осуществляется переход к следующему виду полос большей ширины. Если число полос этого вида не равно нулю, оно уменьшается на единицу, после чего рассчитываются новые значения числа полос предпоследнего и последнего вида, число полос остальных видов не меняется. В противном случае осуществляется переход к следующему виду полос большей ширины и т.д.
Обозначим p l, l = 1,..., k - число полос l -го вида в последнем из сформированных вариантов; q l, l = 1,..., k - число полос l -го вида в очередном формируемом варианте. Значения q l, l = 1,..., k рассчитываются по следующим формулам (для удобства понимания формулы записаны в порядке убывания индекса l; значение “ост” означает вычисление по “остаточному принципу”):
qk = “ост”
qk-1 = если p k-1 > 0, то p k-1 - 1;
иначе “ост”
qk-2 = если p k-1 > 0, то p k-2;
иначе, если p k-2 > 0, то p k-2 - 1;
иначе “ост”
qk-3 = если p k-1 > 0 или p k-2 > 0, то p k-3;
иначе, если p k-3 > 0, то p k-3 - 1;
иначе “ост”
...................................
q2 = если p k-1 > 0 или p k-2 > 0 или... или p3 > 0, то p2;
иначе, если p2 > 0, то p2 - 1;
иначе “ост”
q1 = если p k-1 > 0 или p k-2 > 0 или... или p2 > 0, то p1;
иначе p1 - 1
Формирование множества допустимых вариантов раскроя заканчивается как только будет получен вариант, в котором из листа (рулона) выкраиваются только полосы последнего типа (наименьшей ширины).
Пакет “Поиск решения” ЭТ Excel позволяет решать задачи линейного и целочисленного программирования с числом неизвестных не более 200. Эту особенность следует учитывать при большом числе допустимых вариантов раскроя. В этом случае следует применять метод случайного поиска в сочетании с “Поиском решения”. На каждом шаге поиска из общего множества допустимых вариантов раскроя случайным образом выбирается 100 вариантов, из которых “Поиск решения” формирует текущий оптимальный план раскроя. Если он оказывается лучшим по величине отходов материала по сравнению с полученными на предшествующих шагах поиска, то этот план запоминается и используется для сравнения на последующих шагах поиска. Проведя достаточно большое число шагов поиска, можно найти план раскроя, близкий к теоретически оптимальному.
Вопросы для самопроверки
1. Сформулируйте постановку базовой задачи раскроя материала, запишите соответствующую ей экономико-математическую модель.
2. Охарактеризуйте задачу раскроя материала с позиций обобщенной модели Л.В. Канторовича.
3. Чем характеризуется каждый вариант раскроя материала? Опишите технологию формирования множества всех допустимых вариантов раскроя.
4. Опишите методику решения задачи раскроя материала при большом числе возможных вариантов раскроя материала.
5. Перечислите цели постоптимизационного анализа решения задачи раскроя материала, опишите методику его проведения.
6. Каким требованиям должен удовлетворять приемлемый в организационном и технологическом отношении план раскроя материала? Опишите методику его формирования.
Date: 2015-06-11; view: 1213; Нарушение авторских прав