Двойственность в линейном программировании

При выявлении и экономической интерпретации особенностей оптимального решения задачи планирования производства, а также при проведении постоптимизационного анализа его устойчивости к возможным изменениям производственной ситуации важную роль играет аппарат теории двойственности линейного программирования.

Суть проблемы двойственности состоит в том, что для каждой задачи линейного программирования можно построить по определенным правилам двойственную задачу. Если эти правила применить к самой двойственной задаче, то образуется исходная задача. Между оптимальными решениями исходной задачи и двойственной к ней существует взаимосвязь, которая описывается теоремами двойственности.

Рассмотрим симметричную пару двойственных задач, приняв в качестве исходной базовую задачу планирования производства. Построим двойственную задачу по следующим правилам: число неизвестных двойственной задачи равно числу основных ограничений исходной задачи и, наоборот, число основных ограничений двойственной задачи равно числу неизвестных исходной задачи; матрица основных ограничений двойственной задачи образуется путем транспонирования соответствующей матрицы исходной задачи; параметрами ограничений (правыми частями) двойственной задачи служат коэффициенты при неизвестных в целевой функции исходной задачи и, наоборот, коэффициенты в целевой функции двойственной задачи совпадают с параметрами ограничений исходной задачи; знаки неравенств основных ограничений двойственной задачи противоположны знакам неравенств основных ограничений исходной задачи; если исходная задача - на максимум, то двойственная к ней - на минимум и, наоборот.

Обозначив через y_i, i=1,..., m неизвестные двойственной задачи, запишем ее математическую модель в виде:

Найти min z =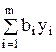

при условиях

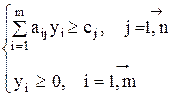
Рассматриваемая двойственная задача интерпретируется как задача об установлении справедливых цен на ресурсы в случае, когда некоторая организация приобретает у предприятия не продукцию, а исходные ресурсы, используемые для ее производства. Интересы организации, приобретающей ресурсы, состоят в минимизации суммарной стоимости ресурсов и представлены целевой функцией двойственной задачи. Интересы предприятия отражены основными ограничениями двойственной задачи, согласно которым стоимость ресурсов по справедливым ценам, затрачиваемых на производство продукции каждого вида, должна быть не менее прибыли от реализации продукции, изготовленной из этих ресурсов.

Подчеркнем условный характер цен ресурсов, определяемых решением двойственной задачи. Они не имеют отношения к рыночным ценам ресурсов и отражают лишь значимость ресурсов в конкретных условиях данной производственной ситуации.

Условные цены ресурсов (называемые также двойственными оценками) служат инструментом постоптимизационного анализа устойчивости оптимального решения задачи о планировании производства при возможных изменениях производственной ситуации: удельной прибыли от реализации продукции, запасов ресурсов, норм затрат ресурсов на производство продукции. При этом используются теоремы двойственности линейного программирования.

Согласно первой теореме двойственности суммарные затраты на приобретение ресурсов по оптимальным ценам равны общей прибыли от реализации всей продукции, изготовленной предприятием при оптимальном плане выпуска продукции из имеющихся запасов ресурсов:

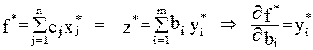
Из первой теоремы двойственности следует, что условные цены ресурсов характеризуют приращение суммарной прибыли на каждую дополнительную единицу запаса соответствующего ресурса.

Вторая теорема двойственности устанавливает соотношения между компонентами оптимальных решений прямой и двойственной задач. Для того, чтобы допустимые решения x₁,x₂,..., x_n; y₁,y₂,..., y_m прямой и двойственной задач были бы их оптимальными решениями, необходимо и достаточно выполнение условий:

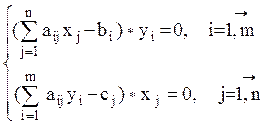
Условиям второй теоремы двойственности можно дать следующую экономическую интерпретацию: i-й вид ресурса имеет ненулевую цену, если полностью расходуется в процессе производства (такой ресурс будем называть дефицитным); j-й вид продукции производится, если стоимость затраченных на его производство ресурсов по оптимальным ценам равна прибыли от реализации данной продукции (такой вид продукции будем называть базисным).

Сравнительно небольшие изменения удельной прибыли или запасов ресурсов не приводят к нарушению условий второй теоремы двойственности, оптимальная номенклатура выпускаемой продукции и состав дефицитных ресурсов остаются неизменными.

Диапазоном устойчивости оптимального плана при изменении удельной прибыли c_j назовем множество значений c_j, при которых остаются неизменными оптимальные объемы выпуска продукции (цены дефицитных ресурсов линейно изменяются при переходе от нижней к верхней границе диапазона устойчивости).

Диапазоном устойчивости оптимального плана при изменении запаса ресурса b_i назовем множество значений b_i, при которых остаются неизменными оптимальные цены ресурсов (оптимальные объемы выпуска базисных видов продукции линейно меняются при переходе от нижней к верхней границе диапазона устойчивости).

Одна из задач постоптимизационного анализа - найти нижние и верхние границы диапазонов устойчивости оптимального решения задачи и выявить лимитирующие факторы, которые приводят к образованию границ диапазонов устойчивости.

Сформулированные выше положения двойственности для базовой задачи планирования производства и симметричной к ней задачи об условных ценах ресурсов остаются в силе и в общем случае, когда имеют место не только потребляемые, но и накапливаемые ингредиенты. При этом потребляемым ингредиентам соответствуют неотрицательные значения условных цен (положительные - для дефицитных ингредиентов, полностью расходуемых в процессе производства, и нулевые - для недефицитных ингредиентов). Накапливаемым ингредиентам соответствуют неположительные значения условных цен. Если при оптимальном плане производства продукции объем накапливаемого ингредиента в точности равен заданному значению, то его условная цена отрицательна (подобная ситуация имеет место при госзаказе на невыгодный для предприятия вид продукции). При превышении заданного объема накапливаемого ингредиента его условная цена равна нулю (установлен госзаказ на выгодный вид продукции, которая производится в объеме, превышающем госзаказ).

Date: 2015-06-11; view: 829; Нарушение авторских прав