Структурный и стоимостной анализ

Ключевым разделом темы является методика проведения постоптимизационного анализа решения задачи планирования производства.

На первом этапе вырабатываются рекомендации о том, как предприятие должно реагировать на случайные (не контролируемые со стороны предприятия) изменения производственной ситуации. С этой целью проводится структурный анализ: рассчитываются альтернативные планы выпуска продукции, которые следует использовать при непредвиденных структурных изменениях производственной обстановки, таких как невозможность использования по тем или иным причинам представленных в теоретически оптимальном плане технологических вариантов выпуска продукции того или иного вида, падение спроса на отдельные виды продукции до нулевого уровня (до объема заказа, если он имеет место для данного вида продукции). Необходимо проанализировать и благоприятные структурные изменения – неограниченное возрастание спроса на те виды продукции, объем выпуска которых в теоретически оптимальном плане ограничен ранее заданным объемом спроса. На основе выполненных расчетов альтернативных планов должны быть обоснованы рекомендации по дополнительной заблаговременной организационно-технологической подготовке производства, обеспечивающей возможность гибкой перестройки планов выпуска продукции при возможных структурных изменениях производственной ситуации.

Полученные рекомендации дополняются результатами стоимостного анализа с использованием понятий диапазонов устойчивости оптимального решения, которые вытекают из второй теоремы двойственности.

Диапазоном устойчивости при варьировании удельной прибыли называется множество значений варьируемого параметра, при которых остается неизменным оптимальный план выпуска продукции, а оптимальные значения суммарной прибыли и условных цен ресурсов линейно изменяются при переходе от левой границы диапазона устойчивости к правой (в частном случае некоторые из них не меняют своих значений внутри диапазона устойчивости).

Принимается, что под действием случайных факторов значения удельной прибыли могут изменяться в пределах ± 30 % от номинальных величин. Если эти изменения выходят за границы диапазонов устойчивости, то следует рассмотреть и оценить два возможных варианта поведения предприятия:

· придерживаться намеченного ранее плана выпуска продукции, который в новых условиях уже не будет оптимальным, а потому нести некоторые дополнительные потери;

· перейти на новый план выпуска продукции, оптимальный для новых условий.

Из указанных двух вариантов первый целесообразно рекомендовать только в том случае, когда потери прибыли малы и при этом требуется существенная перестройка производства для реализации плана, соответствующего второму варианту.

Практическим итогом первого этапа постоптимизационного анализа являются рекомендации по дополнительной заблаговременной организационно-технологической подготовке производства продукции на случай возможных изменений производственной ситуации, которые позволят свести к минимуму потери прибыли при неблагоприятных изменениях производственной ситуации и в максимальной степени использовать благоприятные изменения.

1.4.2. Формирование целочисленного плана выпуска
продукции

На втором этапе постоптимизационного анализа формируется целочисленный план выпуска продукции, приемлемый с точки зрения организации производства и не слишком сильно отличающийся от теоретически оптимального решения по суммарной прибыли.

Приемлемым с точки зрения организации производства следует считать такой план, в котором объемы выпуска продукции представлены целочисленными значениями, кратными установленному размеру партии, например, 10, 20 или 50 единицам продукции. Кроме того, такой план не должен включать малообъемные компоненты, т.е. должны быть установлены пороговые значения, ограничивающие снизу ненулевые объемы выпуска продукции, предлагаемой для производства. Для формирования производственного плана, обладающего указанными свойствами, используется экономико-математическая модель задачи планирования производства с комплектным выпуском продукции. Базовая (одноиндексная) модель рассматриваемой задачи записывается в виде:

Найти max f =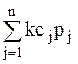

при условиях

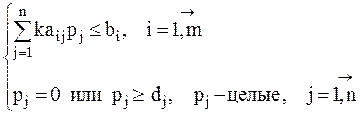
Наряду с обозначениями, принятыми ранее для базовой нецелочисленной задачи планирования производства (с. 10), здесь используются следующие обозначения:

k – размер партии;

dj, j=1,..., n – минимально допустимое число производимых партий продукции j-го вида;

pj, j=1,..., n – число производимых партий продукции j-го вида (неизвестные, оптимальные значения которых определяются при решении задачи).

Данная задача представляет собой задачу целочисленного программирования. Для решения линейных задач целочисленного программирования успешно применяется метод ветвей и границ, который реализован в пакете “Поиск решения” электронной таблицы Excel (наряду с симплексным методом линейного программирования и некоторыми методами решения задач нелинейного программирования). Это позволяет в автоматическом режиме решать задачи целочисленного линейного программирования. Рассмотренная выше задача формирования целочисленного плана выпуска продукции не является задачей целочисленного линейного программирования. Наличие пороговых значений неизвестных выводит ее из класса задач целочисленного линейного программирования. Тем не менее, данная задача может быть сведена к последовательности порожденных задач целочисленного линейного программирования, каждая из которых формируется в интерактивном режиме с учетом ограничений, связанных с пороговыми значениями объемов выпуска продукции.

Опишем методику решения целочисленной задачи планирования производства с пороговыми значениями объемов выпуска продукции, ориентированную на применение пакета “Поиск решения” в интерактивном режиме. Введем понятия текущего, допустимого и приемлемого плана рассматриваемой задачи.

Текущим планом будем называть целочисленный план, оптимальный для базовых ограничений задачи планирования производства и некоторой совокупности дополнительных ограничений, сформированных пользователем в интерактивном режиме.

Допустимым будем называть текущий план, удовлетворяющий всем ограничениям, связанным с пороговыми величинами объемов выпуска продукции.

Приемлемым назовем текущий план, для которого потери прибыли по сравнению с теоретически оптимальным решением не превышают установленной величины и которому соответствует лучшая величина суммарной прибыли, чем найденному ранее допустимому плану. Если приемлемый план не является допустимым, то путем дробления соответствующей ему порожденной задачи потенциально возможно получить допустимый план с лучшей величиной суммарной прибыли по сравнению с найденным ранее допустимым планом.

Решить сформулированную выше целочисленную задачу планирования производства – это значит выявить все допустимые планы и выбрать лучший из них по величине суммарной прибыли.

Пакет “Поиск решения” позволяет находить текущий план для заданной совокупности ограничений, указанных в диалоговом окне настроек пакета. Меняя настройки пакета и запуская его повторно, можно в интерактивном режиме целенаправленно формировать множество текущих планов с целью выявления среди них всех допустимых планов и выбора лучшего по величине суммарной прибыли.

Решение целочисленной задачи планирования производства с пороговыми значениями объемов выпуска продукции начинается с определения текущего плана для базовой системы ограничений, включающей условие целочисленности значений неизвестных. Если получен приемлемый допустимый план, то задача решена. Если получен допустимый план, не являющийся приемлемым, то задача решения не имеет. Наконец, если текущий план для исходной задачи оказался приемлемым, но недопустимым, то реализуется алгоритм целенаправленного перебора текущих планов, связанный с формированием и решением множества порожденных задач.

Для целенаправленного перебора текущих планов используется тот же метод ветвей и границ, который применяется в пакете “Поиск решения” для поиска оптимального плана задачи целочисленного линейного программирования.

Если на некотором шаге в результате решения одной из порожденных задач получен неприемлемый текущий план, то убивается соответствующая ему ветвь иерархической структуры порожденных задач.

Если получен приемлемый, но недопустимый план, в котором положительная компонента pjменьше порогового значения dj, то производится дробление очередной задачи на две порожденные задачи: в систему ограничений вводится дополнительное условие pj= 0 для первой из пары порожденных задач и условие pj³ djдля второй порожденной задачи. Каждая из порожденных задач является задачей целочисленного линейного программирования и решается с помощью пакета “Поиск решения” после интерактивного уточнения настроек в диалоговом окне пакета.

Если на данном шаге впервые получен допустимый план, то он запоминается вместе с соответствующей ему величиной суммарной прибыли. Если же ранее уже был найден допустимый план с лучшей величиной суммарной прибыли, то убивается ветвь иерархической структуры порожденных задач, соответствующая вновь найденному допустимому плану. В противном случае запоминается новый допустимый план и убивается ветвь ранее найденного допустимого плана.

Процедура решения исходной задачи заканчивается, когда в иерархической структуре порожденных задач остается единственная ветвь, соответствующая лучшему из найденных допустимых решений.

Продемонстрируем методику формирования целочисленного плана выпуска продукции на примере тестовой задачи с дополнительными условиями:

· продукция производится партиями размером 10 ед.;

· пороговая величина объема выпуска продукции по каждому технологическому варианту для первого, второго и четвертого видов продукции равна 100 ед. (10 партий); для продукции третьего вида в соответствии с ограничением спроса пороговая величина объема выпуска равна 60 ед. (6 партий);

· при использовании целочисленного плана выпуска продукции потери прибыли не должны превышать 5% по сравнению с теоретически оптимальным решением.

Несмотря на то, что математическая модель тестовой задачи отличается от базовой одноиндексной модели, рассмотренная методика применима для решения тестовой целочисленной задачи планирования производства. На рис. 5 показана компоновка листа ЭТ Excel с настройками нулевого и первого шага для ее решения.

На нулевом шаге к ограничениям исходной задачи добавляется лишь требование целочисленности значений числа производимых партий продукции. Полученное решение (здесь и в дальнейшем показываем только ненулевые компоненты текущих планов):

p1_2 = 12, p2_2 = 12, p3_1 = 5, p4_3 = 18,

f = 76000 (потери прибыли 0,6%)

представляет собой приемлемый, но недопустимый текущий план, так как значение p3_1 меньше пороговой величины, установленной для третьего вида продукции.

Производим дробление задачи нулевого шага на две порожденные задачи и приступаем к решению первой из них, вводя дополнительное ограничение p3_1 ³ 6 (что соответствует настройке ЭТ: $F$7>=6). В дальнейшем, закончив решение первой задачи (с возможными дроблениями на новые порожденные задачи), вернемся ко второй из этой пары порожденных задач нулевого шага и заменим дополнительное ограничение на p3_1 = 0.

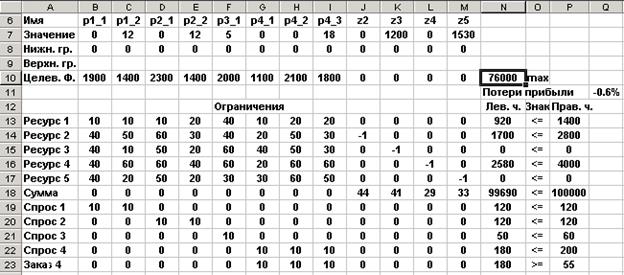
0 шаг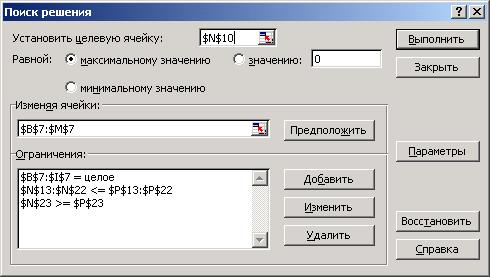

1 шаг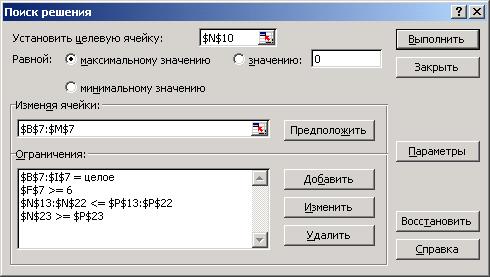

Рис. 5. Компоновка листа ЭТ Excel и настройка пакета “Поиск решения” для целочисленной задачи планирования производства

Полный сценарий решения рассматриваемой целочисленной задачи выглядит следующим образом.

0 шаг p1_2 = 12, p2_2 = 12, p3_1 = 5, p4_3 = 18,

f = 76000 (потери прибыли 0,6%)

Текущий план является приемлемым, но недопустимым, производится дробление текущей задачи на две порожденные задачи с дополнительными ограничениями p3_1 ³ 6 и p3_1 = 0 соответственно.

1 шаг p3_1 ³ 6

p1_2 = 12, p2_1 = 1, p2_2 = 11, p3_1 = 6, p4_3 = 16,

f = 75300 (потери прибыли 1,5%)

Текущий план является приемлемым, но недопустимым, производится дробление текущей задачи на две порожденные задачи с дополнительными ограничениями p2_1 = 0 и p2_1 ³ 10 соответственно.

2 шаг p3_1 ³ 6, p2_1 = 0,
p1_2 = 12, p2_2 = 11, p3_1 = 6, p4_2 = 1, p4_3 = 16,

f = 75100 (потери прибыли 1,8%).

Получен приемлемый, но недопустимый план, производится дробление текущей задачи на две порожденные задачи с дополнительными ограничениями p4_2 = 0 и p4_2 ³ 10 соответственно.

3 шаг p3_1 ³ 6, p2_1 = 0, p4_2 = 0
p1_1 = 1, p1_2 = 11, p2_2 = 12, p3_1 = 6, p4_3 = 16,

f = 74900 (потери прибыли 2,0%).

Получен приемлемый, но недопустимый план, производится дробление текущей задачи на две порожденные задачи с дополнительными ограничениями p1_1 = 0 и p1_1 ³ 10 соответственно.

4 шаг p3_1 ³ 6, p2_1 = 0, p4_2 = 0, p1_1 = 0

p1_2 = 11, p2_2 = 12, p3_1 = 6, p4_3 = 17,

f = 74800 (потери прибыли 2,1%).

Получен первый допустимый план, с которым далее будут сравниваться другие текущие планы.

5 шаг p3_1 ³ 6, p2_1 = 0, p4_2 = 0, p1_1 ³ 10
p1_1 = 10, p1_2 = 2, p2_2 = 12, p3_1 = 6, p4_3 = 10,

f = 68600 (потери прибыли 10,3%).
Получен неприемлемый план, ветвь убивается.
6 шаг p3_1 ³ 6, p2_1 = 0, p4_2 ³ 10
p1_2 = 12, p2_2 = 12, p3_1 = 6, p4_1 = 1, p4_2 = 10, p4_3 = 12

f = 71300 (потери прибыли 6,7%).
Получен неприемлемый план, ветвь убивается.

7 шаг p3_1 ³ 6, p2_1 ³ 10
p1_2 = 12, p2_1 = 10, p2_2 = 2, p3_1 = 6, p4_3 = 9

f = 70800 (потери прибыли 7,4%).
Получен неприемлемый план, ветвь убивается.

8 шаг p3_1 = 0

p1_2 = 12, p2_1 = 5, p2_1 = 7, p4_3 = 20,

f = 74100 (потери прибыли 3,1%)

Получен неприемлемый план ввиду меньшей прибыли по сравнению с полученным ранее допустимым планом. Ветвь убивается.

В структуре множества порожденных задач остается одна ветвь, конечным элементом которой является порожденная задача, сформированная на
4-м шаге. Ее оптимальный план является решением исходной задачи

. На рис. 6 приведена иерархическая структура сформированного и проанализированного множества порожденных задач.

На схеме рис. 6 в вершинах указаны номера шагов, на которых получены соответствующие текущие планы, а рядом со стрелками – дополнительные ограничения для порожденных задач.

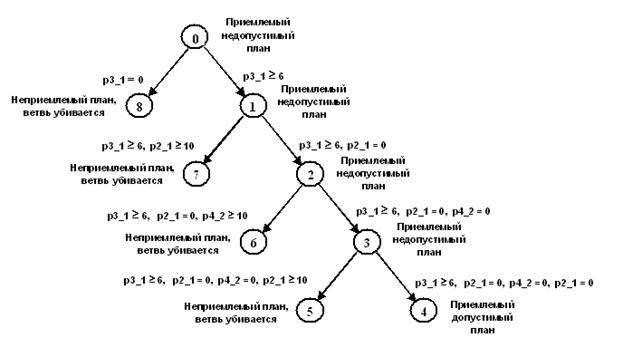
Рис. 6. Иерархическая структура множества порожденных задач
для тестового примера

Date: 2015-06-11; view: 564; Нарушение авторских прав