Компьютерные методы решения

Для решения задачи планирования производства используется пакет “Поиск решения”, являющийся одной из надстроек электронной таблицы Excel. Достоинством пакета “Поиск решения” является простота и удобство подготовки исходных данных, возможность получения целочисленного решения, использование встроенных средств Excel для постоптимизационного анализа и наглядного представления полученных результатов в виде таблиц, графиков и диаграмм.

На рис. 2 представлена компоновка листа ЭТ Excel с исходной информацией для решения тестовой задачи планирования производства и настройки пакета “Поиск решения”. Диапазон ячеек B5:M5 отводится для значений неизвестных - объемов выпуска продукции x_1,1, x_1,2, …, x_4,3 и объемов дополнительно приобретаемых ресурсов z₂, …, z₅. Исходные значения неизвестных установлены равными нулю. В диапазон B8:M8 заносятся коэффициенты при неизвестных в целевой функции – значения удельной прибыли для объемов выпуска продукции и нули для объемов дополнительно приобретаемых ресурсов.

Ячейка N8 содержит формулу

=СУММПРОИЗВ(B$5:M$5;B8:M8)

для вычисления суммарной прибыли как скалярного произведения строки значений неизвестных со строкой коэффициентов при неизвестных в целевой функции.

В диапазоне B11:M21 содержатся коэффициенты при неизвестных в левых частях ограничений математической модели тестовой задачи планирования производства, в том числе нормы расхода ресурсов (диапазон B11:I15), рыночные цены ресурсов (диапазон J16:M16). Значения “–1” в ячейках J12, K13, L14, M15 являются результатом переноса в левые части соответствующих неравенств неизвестных z₂, …, z₅, которые в математической модели записаны в правых частях. Значения 1 в ячейках B17, C17, D18 и др. отображают нормы участия отдельных технологических вариантов в суммарных объемах выпуска продукции соответствующих видов.

В ячейки диапазона N11:N21 копируется формула из ячейки N8, что позволяет вычислять левые части ограничений - объемы ингредиентов, соответствующие текущим значениям неизвестных x_1,1, x_1,2, …, x_4,3, z₂, …, z₅. В ячейки диапазона P11:P21 записываются исходные значения правых частей ограничений – запасы ресурсов, сумма средств на приобретение дополнительных ресурсов, объемы спроса, объем госзаказа.

После занесения на лист Excel исходных данных для решения задачи планирования производства и формул, вычисляющих значения целевой функции и левых частей ограничений, производится настройка пакета “Поиск решения” в диалоговых окнах показанных в нижней части рис. 2. Указывается ячейка целевой функции $N$8, значение которой максимизируется. Указывается диапазон ячеек $B$5:$M$5 для значений неизвестных. Записываются ограничения для потребляемых ингредиентов – объемов ресурсов, суммы средств на приобретение ресурсов, объемов спроса – в виде неравенств

$N$11:$N$20 <= $P$11:$P$20.

Для накапливаемого ингредиента – госзаказа – ограничение записывается в виде неравенства

$N$21 >= $P$21.

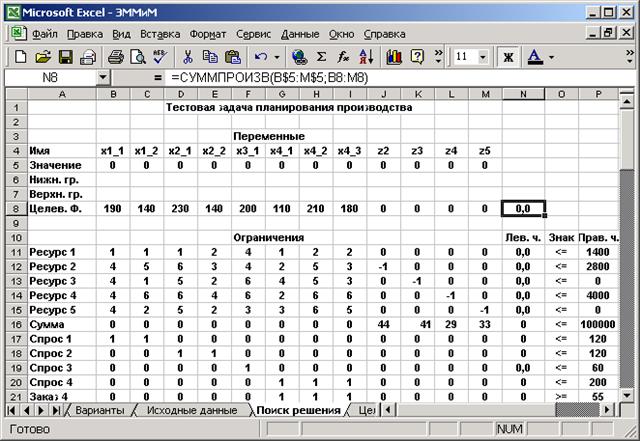
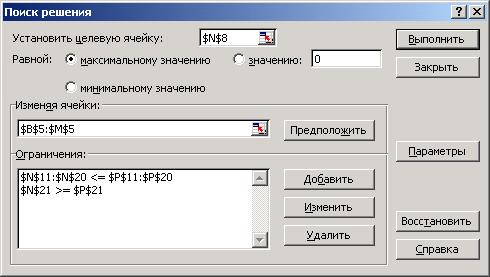
Рис. 2. Компоновка листа ЭТ Excel и настройки пакета “Поиск решения” для тестовой задачи планирования производства

В дополнительном окне настроек задаются методы и требования по точности вычислений. Установленная опция “Линейная модель” предписывает применять для решения задачи симплексный метод линейного программирования. Опция “Неотрицательные значения” устанавливается для учета дополнительных условий неотрицательности значений неизвестных.

На рис. 3 представлены результаты решения тестовой задачи планирования производства пакетом “Поиск решения”. В диалоговом окне сообщается, что все заданные условия выполнены и найдено оптимальное решение. При выборе опции “Сохранить найденное решение” на место исходных значений неизвестных (диапазон ячеек $B$5:$M$5) пакет записывает их оптимальные значения, при этом в ячейке целевой функции $N$8 отображается ее оптимальное значение, а в ячейках диапазона $N$11:$N$21 – значения левых частей ограничений (объемов ингредиентов) при оптимальном решении.

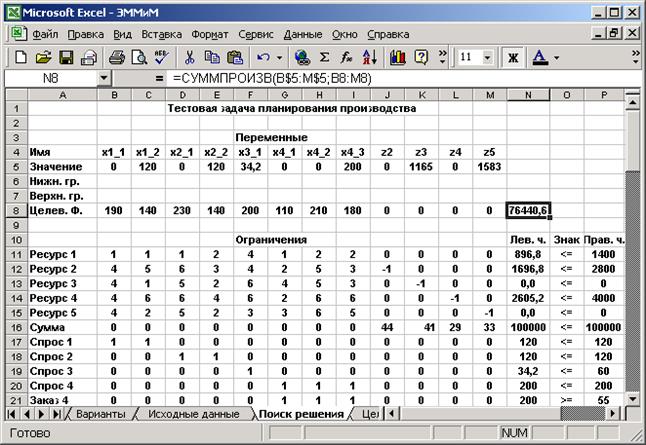
Рис. 3. Решение тестовой задачи, полученное пакетом “Поиск решения”

Более подробную информацию об оптимальном решении можно получить с помощью формируемых пакетом отчетов “Результаты”, “Устойчивость” и “Пределы”, показанных в диалоговом окне на рис. 3. Фрагмент отчета “Устойчивость”, содержащий двойственные оценки неизвестных (в терминологии пакета “нормированные стоимости”) и условные цены ресурсов (в терминологии пакета “теневые цены”) представлен на рис. 4. Там же приведены диаграммы, иллюстрирующие положения первой теоремы двойственности и показывающие вклад базисных видов продукции и дефицитных ресурсов в суммарную прибыль.

Рис. 4. Фрагменты отчета “Устойчивость” и диаграммы распределения

суммарной прибыли по видам продукции и видам ресурсов

Для рассматриваемой тестовой задачи оптимальный план производства включает все четыре вида продукции. Ресурсы первого, второго и четвертого видов не полностью используются в процессе производства (являются недефицитными). Вся выделенная сумма расходуется на приобретение дефицитных ресурсов третьего и пятого видов.

Продукция первого, второго и четвертого вида производится в объеме спроса на эти виды продукции. Спрос на продукцию третьего вида удовлетворяется не полностью, что связано с ограниченной суммой средств для приобретения дефицитных ресурсов третьего и пятого видов. Обратим внимание на то, что представленные в оптимальном плане технологические варианты выпуска продукции первого, второго и четвертого вида характеризуются не самыми большими значениями удельной прибыли. Это связано с тем, что конкурентоспособность того или иного технологического варианта определяется соотношением удельной прибыли и норм затрат дефицитных ресурсов и выявляется в процессе решения задачи.

1.4. Постоптимизационного анализа решения задачи
планирования производства

Date: 2015-06-11; view: 509; Нарушение авторских прав