Краткое изложение основ теории вероятностей

Основные понятия и определения

Испытанием (опытом) называется одно из сколь угодно большого числа раз воспроизводимого определённого перечня (состава) условий.

Событие – совокупность явлений, происходящих в результате испытания.

Если событие происходит неизбежно в результате каждого испытания, оно называется достоверным.

Если событие не может произойти, оно называется невозможным.

Множество возможных при данном испытании и связанных с ним событий называется полем событий, а события этого поля суть случайные события.

Случайное событие – всякий факт (исход), который может произойти или не произойти.

Выборкой называется небольшая часть некоторого множества объектов, отобранная наугад. При этом отобранные объекты правильно отражают качества и свойства элементов множества, что достигается в результате тщательного предварительного перемешивания (диспергирования свойств). Отбор каждого элемента выборки является испытанием и завершается соответствующим событием.

Выборка с возвращением – при последовательном выборе шаров из урны после каждого выбора взятый шар возвращается в урну.

Выборка без возвращения – из урны выбирается некоторое количество шаров без возвращения.

Пусть n – число элементов выборки от 1 до n. Осуществление выборки представляет собой поле событий

А₁, А₂,… А_n, (2.1)

где А_n – отбор n – го элемента, а события поля равновозможны.

События поля могут быть э лементарными и сложными. Сложному событию А_n{n₁, n_2, … n_k}, где n₁ < n₂ <…< n_k – номера элементарных событий, составляющих сложное, соответствует появление событий с номерами n₁ или n₂, …, или n_k. Здесь каждому событию А _n соответствует некоторое количество (или подмножество) элементарных событий.

Говорят, что событие А влечёт за собой событие В (из А следует В), если при наступлении А неизбежно наступление В.

Если из А следует В и одновременно из В следует А, то события А и В эквивалентны или А=В.

Каждое событие поля представляет собой подмножество некоторых событий из множества (А₁, А₂,… А_n,). Например, событие В, состоящего в появлении номеров 2, 5, 7, принято обозначать В {2, 5, 7}. Его записывают как логическую сумму

В = А₂+ А₅+ А₇, (2.2)

где «+» равнозначен союзу «или».

В данном случае можно событие В представить как сумму двух событий

В = {2, 5 }+{7}

или В = (А₂+ А₅) + А₇. (2.3)

Событие В является также суммой несовместных событий, так как события {2, 5} и {7} не могут произойти в одном испытании. Совместными являются события {1, 2, 3, 4} и {4, 5, 6, 7}, они наступают вместе в тех испытаниях, в которых появляется номер 4. Сумма {1, 2, 3} + {1, 2} тождественна событию {1, 2, 3}.

Сумма любых двух событий поля есть событие того же поля.

Полю всегда принадлежит достоверное событие S {1, 2, … n },заключающееся в том, что выбирается один из номеров от 1 до n. События «- n»,… «- 1 », 0, n+ 1 – невозможны и обозначаются 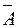(«не А»).

События А и 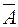– взаимно дополнительны или противоположны, если они несовместны и составляют в сумме достоверное событие, то есть достоверно то, что наступит А или .

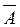Под произведением событий А₁, А₂,… А_n, понимается одновременное наступление их всех, то есть когда А₁ и А₂ и … и А_n наступают вместе.

Произведением двух событий С { 1, 2, 3, 4 } и D { 2, 4, 6, 8 } является событие Е= СD ={2, 4}.

Date: 2015-07-17; view: 969; Нарушение авторских прав