Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?
Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника
Законы распределения случайной величины
|
|
Законом распределения вероятности случайной величины называется всякое соотношение, устанавливающее связь между возможными значениями случайной величины и соответствующими им вероятностями.
Для получения закона распределения используются три способа:
· 
|
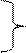
· графический (см. рис.2.1)
· аналитический – для непрерывных величин
табличный закон распределения
Таблица 2.1
| A. Х | х 1 | х 2 | х 3 | … | х n |
| P (X) | P (x 1) | P (x 2) | P (х 3) | … | P (х n) |
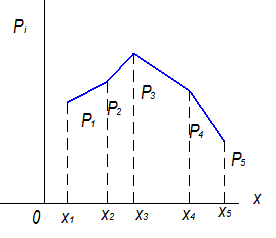
Для непрерывных величин табличный способ не применяется. Непрерывные случайные величины задаются функцией распределения:
F (x) = P (x 1 ,¥)
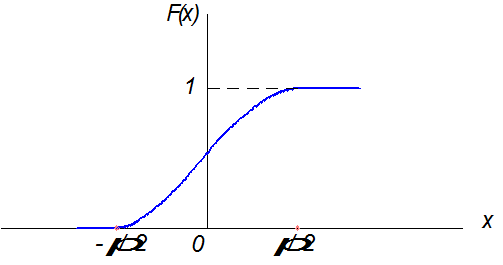
Функция распределения имеет ряд свойств:
Она является функцией неубывающей
0 £ F (x) £ 1
Плотность распределения («плотность вероятности»): – первая производная от функции распределения. Другие названия: «дифференциальная функция распределения», «дифференциальный закон распределения»
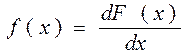(2.25)
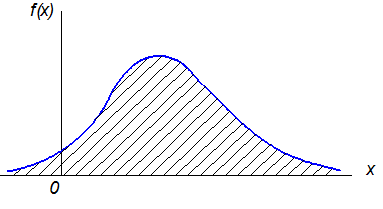
Рис. 2.3 Плотность распределения
Плотность распределения изображается кривой распределения и показывает, как по оси абсцисс распределяются массы, то есть кривая проходит через концы абсцисс значений «линейной плотности».
.
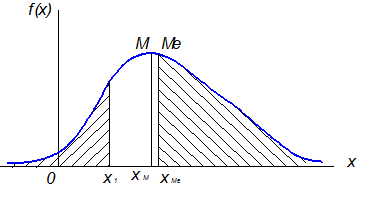
Рис. 2.4. Определение функции распределения
Функция распределения в интервале от 0 до х1 (рис.2.4) определяется как интеграл плотности распределения
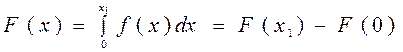(2.26)
Модой случайной величины называется то её значение, в котором плотность вероятности наибольшая (т. М на рис.2.4), т. М является точкой перегиба кривой.
Медианой случайной величины Х называется такое её значение, для которого ограниченная кривой распределения площадь делится пополам (т. Ме на рис.2.4). Площади справа и слева от медианы равны.
Date: 2015-07-17; view: 887; Нарушение авторских прав