Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?
Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника
Теорема сложения вероятностей
|
|
Вероятность появления какого-либо из нескольких несовместных событий равна сумме вероятностей каждого из этих событий:
Р (А1 + А2 + … + Аk) = 
Р (А1) + Р (А2) + … + Р (Аk). (2.12)
Следствие 1:
– Сумма вероятностей всех возможных событий, составляющих данное событие, равна единице.
Следствие 2:
– Сумма вероятностей двух противоположных событий равна единице.
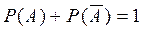. (2.13)
Условная вероятность события А при наступлении события В – вероятность события А, вычисленная в предположении, что событие В произошло:
P (А /В) = P (АВ) /P (В) (2.14)
Теоремы умножения вероятностей
Теорема умножения вероятностей зависимых событий:
Р (АВ) = Р (В) × Р (А/В) (2.15)
Теорема умножения вероятностей независимых событий:
Р (АВ) = Р (А) × Р (В) (2.16)
На основании теорем сложения и умножения вероятностей составляется общее правило сложения вероятностей: вероятность суммы двух событий (совместных или несовместных) равна сумме вероятностей этих событий без вероятности совместного их наступления
P (A+B) = P (A) + P (B)- P (AB). (2.17)
Для несовместных событий P (AB)=0, и (2.17) приводится к (2.12)
Date: 2015-07-17; view: 717; Нарушение авторских прав