Найімовірніше число випробувань в схемі Бернуллі.

Найімовірнішим числом m0 появи події А в n незалежних випробовуваннях називається число, для якого ймовірність не менша ймовірності кожного з решти можливих варіантів, тобто

Якщо найімовірніше число, то повинні виконуватись такі умови:

1.

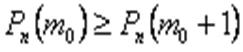
2.

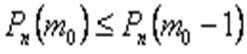
З нерівності (1) отримується:

звідки (після скорочень)

Розв’язуючи нерівність відносно m0, отримують:

Аналогічно з нерівності (2) отримується:

Звідки

(4)

Остаточно отримується нерівність:

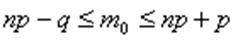!!!!!!!!!!!!!!! (5)

Зауваження. Довжина інтервалу, що визначається нерівністю (5), рівна одиниці:

тому, коли межі інтервалів є дробові числа, то отримується одне значення наймовірнішого числа, якщо ж межі є цілими числами, то отримується два значення наймовірнішого числа успіхів

11. Локальна теорема Муавра-Лапласа:

Якщо , тоді , де

, де (функція Лапласа)

12. Інтегральна теорема Муавра-Лапласа:

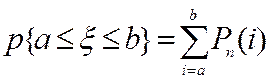
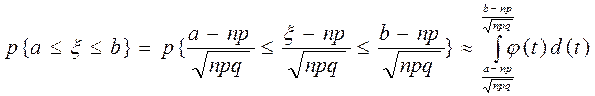
– інтегральна функція Лапласа

,

Використовується якщо.

Теорема Пуассона.

Якщо , то

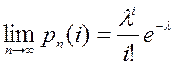
, Випадкова величина x, яка набуває значень 0, 1,..., k,... має розподіл Пуассона з параметром l >0, якщо

.

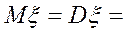
Використовується якщо .

Date: 2016-08-31; view: 269; Нарушение авторских прав