
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Формула повної ймовірності. Формула Байєса
|
|
Повна група подій. Випадкові події H1, …, Hn (Hi ÎÁ, i = 1,… n) утворюють повну групу подій, якщо:
1) Hi — попарно несумісні (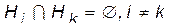 );
);
2) 
Формула повної ймовірності. Якщо H 1, …, Hn — повна група подій і P (Hi)>0 (i = 1,…, n), то для будь-якої події A (A ÎÁ) виконується рівність:
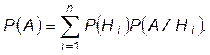
Формула повної ймовірності справджується і для зліченної кількості подій.
Формула Байєса. Якщо H 1, …, Hn — повна група подій, P (Hi)>0 (i = 1,…, n), а A — довільна випадкова подія (A ÎÁ ), з P (A)>0, то
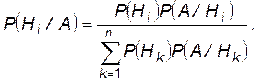
9.Послідовність незалежних випробувань.Схема Бернуллі.
Біноміальний розподіл. Проводяться незалежні випробування; в кожному випробуванні може бути два результати: «успіх» — з ймовірністю p, або «невдача» — з ймовірністю q =1– p. Нехай проведено n випробувань. Позначимо через число «успіхів», тоді
Pn (k) = P {x= k }=  (k =0, 1,..., n).
(k =0, 1,..., n).
Розподіл випадкової величини x називається біноміальним розподілом Бернуллі, а описана вище схема носить назву схеми незалежних випробувань, або схеми Бернуллі.

Date: 2016-08-31; view: 373; Нарушение авторских прав