Производные элементарных функций.

Выведем теперь таблицу производных от элементарных функций

1.

Действительно, если , то

2.

Имеем

вынесем вверху за скобки

Сделаем “замену переменных” . Тогда и

Так как мы получили один из замечательных пределов. Рекомендуется запомнить некоторые частные случаи этой функции этой формулы

а)

б)

3.

Имеем

так как мы снова имеем один из замечательных пределов.

Особенно простой результат получается при

4.

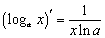
сделаем “замену переменных” . Тогда и

Особенно простой результат получается при

5.

Имеем

где так же использован замечательный предел.

6.

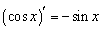
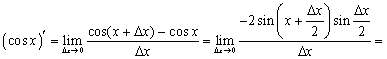
7.

Так как , то

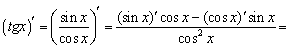
8.

Вывод аналогичен

9.

В данном случае и , т.е. . Поэтому

10.

Вывод аналогичен

11.

В данном случае и , т.е. . Поэтому

12.

Вывод аналогичен

13.

Действительно

14. 15.

Вывод аналогичен

Полученные производные сведены в таблицу 2

функция	производная	функция	производная
1.		6.
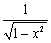
2.		7. arccos x
		
		
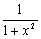
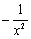
3.		8.
		
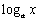
4.		9.
5.




Эти производные называют табличными

Особые случаи

То, что в точке 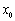функция непрерывна не означает, разумеется, что в этой точке у нее обязательно существует производная. Функция может быть непрерывной, а производной может и не существовать. Что же там может быть?

1. А. Односторонние производные

Назовем

производной от функции в точке 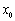слева, а

производной в той же точке справа. Разумеется, если , то это означает, что в точке 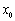существует 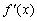. Но могут быть случаи, когда и существуют, но не равны друг другу. В этом случае не существует и 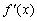. График функции имеет в точке 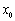в этом случае “излом”, и в этой точке к графику можно провести две касательные.

1. Б. Бесконечная производная

Рассмотрим функцию определенную для и потребуем найти . Имеем

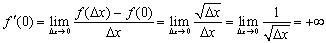
и производная равна .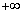

Рассматривая график функции 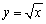легко увидеть, что это означает просто то, что в точке касательная к графику параллельна оси OY.

Date: 2016-08-30; view: 330; Нарушение авторских прав