Теоремы Ферма и Ролля

Теорема Ферма. Пусть функция определена и непрерывна на промежутке 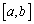и в некоторой внутренней точке 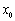этого промежутка достигает своего наибольшего или наименьшего значения, если в этой точке существует производная, то она равна нулю: .

Доказательство

Пусть, для определенности, в точке 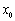функция достигает своего наибольшего значения.

По условию теоремы эта точка внутренняя, т.е. , и поэтому к этой точке можно подойти и слева и справа.

Пусть мы подходим к 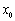слева. Тогда

(т.к. - наибольшее значение)

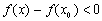
(т.к. мы подходим слева)

Делая предельный переход получим

Пусть мы подходим к точке 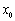справа. Тогда

(т.к. - наибольшее значение)

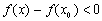
(т.к. мы подходим слева)

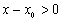
Делая предельный переход получим

Совместить два полученных неравенства можно только в одном случае: . ч.т.д.

Геометрический смысл доказанной теоремы ясен из рисунка: в точке наибольшего или наименьшего значения функции касательная к графику функции параллельна оси OX.

Теорема Ролля. Пусть функция

а) определена и непрерывна на ;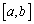

б) ;

в)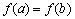

Тогда существует точка в которой .

Доказательство этой теоремы следует из такой логической цепочки рассуждений:

1. Так как определена и непрерывна на 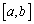, то, по первой теореме Вейерштрасса, она ограничена на 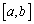, т.е. существуют конечные и .

2. Если , то есть константа, т.е. и поэтому . В качестве точки c можно взять любую точку из .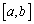

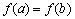3. Если , то, в силу условия и второй теоремы Вейерштрасса, хотя бы одно из значений или достигается во внутренней точке промежутка 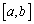,по теореме Ферма, в этой точке (их может быть и две) производная равна нулю.

ч.т.д.

Дифференциал

Рассмотрим важное понятие дифференциала.

Напомним, что величина называется приращением функции.

Определение 1. Функция называется дифференцируемой в точке , если ее приращение можно представить в виде

Определение 2. Линейная часть приращения функции, т.е. называется дифференциалом функции и обозначается

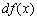
Чтобы точно уяснить эти определения функции рассмотрим пример. Пусть 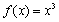. Тогда

Заметим, что содержит слагаемое, линейное по , слагаемые с и . Так вот, только слагаемое, линейное по дает дифференциал, т.е.

1. Теорема о дифференцируемости функций

Для того, чтобы функция была дифференцируемой в точке , необходимо и достаточно, чтобы в этой точке существовала производная 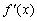. При этом .

Доказательство

Необходимость. Пусть дифференцируема в точке . Это значит, что

Деля на

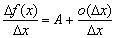
и переходя к пределу , получим

Достаточность. Пусть в точке существует производная

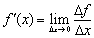
Это, по определению, означает, что

где - бесконечно малая величина. Отсюда следует, что

Но 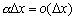и поэтому

что и требовалось доказать.

1. Выражение для дифференциала

Итак, мы получили, что для дифференцируемой функции . Это означает, что

.

Но если взять , то мы получим, что , т.е. дифференциал независимой переменной равен ее приращению. Поэтому окончательно

Отсюда следует, что

т.е. производная есть отношение дифференциала функции к дифференциалу независимой переменной. Заметьте, что есть обычная дробь и с ней можно обращаться как с обычной дробью.

1. Геометрический смысл дифференциала

Вспомним, что 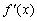есть тангенс угла наклона касательной к оси OX. Поэтому, если провести касательную к кривой в точке , то 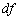будет катетом, который противолежит углу в треугольнике, гипотенуза которого образована касательной, а другой катет есть приращение На рисунке нарисован и отрезок ∆ f (x), так что видно отличие ∆ f (x) и .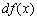

Date: 2016-08-30; view: 559; Нарушение авторских прав