Уравнения, допускающие понижение порядка

Рассмотрим некоторые виды дифференциальных уравнений высших порядков, допускающих понижение порядка.

1. Общее решение уравнения вида может быть получено путем n – кратного последовательного интегрирования.

2. Уравнение n - го порядка вида

не содержащее явно искомой функции и её производных до (к -1) - го порядка, с помощью замены допускает понижение порядка уравнения на к единиц.

3. Уравнение вида

не содержащее явно независимой переменной x, допускает понижение порядка на единицу подстановкой Действительно, имеем

и т.д.

4. Уравнение вида

,

т.е., левая часть представляет полную производную по переменной х от некоторой функции Интегрируя по х порядок уравнения понижается на единицу.

5. Уравнение однородное относительно , то есть

Далее используя подстановку 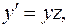порядок исходного уравнения понижают на единицу.

Теперь рассмотрим следующие задачи на использование вышеприведенных теоретических положений.

Задача 1. Найти решение уравнения удовлетворяющее начальным условиям Уравнение явно не содержит переменную x, т.е., имеем случай 3. Полагая в данном уравнении, получим уравнение первого порядка

или

Интегрируем

Отсюда с учетом начальных условий и , при получим

То есть,

Интегрируя, имеем

Полагая у =1 и , находим .

Итак, Отсюда

Задача 2. Найти общее решение уравнения

Имеем случай 1. Интегрируя, находим . Повторно интегрируя, будем иметь Интеграл находим по формуле интегрирования по частям

Положим:

u = arctgx, dv = dx. Тогда

Итак,

Задача 3. Найти общее решение уравнения

Представляет случай 2. Положим

Теперь уравнение принимает вид

Разделяем переменные

Далее, интегрируя, находим

Отсюда Итак,

Легко убедиться, что выражает решение и при Поэтому можно считать, что принимает любые вещественные значения.

Дважды интегрируя по частям, окончательно получим

где - произвольные постоянные.

Задача 4. Найти общее решение уравнения

Это уравнение можно преобразовать к такому виду, чтобы обе его части являлись полными производными по х от некоторых функций.

Действительно, имеем

или

После двукратного интегрирования получим

Тем самым

Положим: u = x, dv = . Отсюда du = dx, Теперь интегрируя по частям, имеем

Положим Тогда общее решение запишется в виде

Задача 5. Найти общее решение уравнения

Уравнение однородное относительно

Положим: 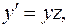где z - новая неизвестная функция от x. Тогда и уравнение принимает вид

Сокращая на , получаем

При этом y = 0 является решением.

Итак, окончательно имеем линейное уравнение Ищем решения в виде Подставляя, будем иметь

Приравняем Разделяем переменные

Подставляя, получаем

Итак, Так как , то приходим к уравнению

Или разделяя переменные, имеем Интегрируем

;

Итак, Если в этом решении возьмем , то получим решение y = 0. Поэтому следует тоже рассматривать в общем интеграле.

Date: 2016-07-25; view: 375; Нарушение авторских прав