Проиллюстрируем на примерах.

а) Проинтегрировать уравнение

.

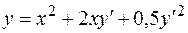Имеем случай 1. Введем параметризацию уравнения, полагая . Тогда . Дифференцируя по переменной x, имеем

или .

Отсюда p = -x + C, p = -2x. Освобождаемся от параметра p, подставляя поочередно оба результата в выражение для y, найдем общее решение

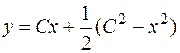и решение .

б) Решить уравнение

.

Имеем случай 2. Положим . Тогда . Дифференцируя по y, получим

или .

Получилось однородное уравнение, кроме того, также является и линейным. Интегрируя, находим . Освобождаясь от параметра p, получим или .

в) Проинтегрировать уравнение

.

Положим . Тогда . Имеем случай 1, кроме того, уравнение не содержащее переменную x. Дифференцируя, получаем

.

Заменяя dy через p dx, затем, интегрируя, находим

.

Можно было бы при решении уравнений вида воспользоваться здесь приведенными зависимостями

, однако, нет в этом необходимости, поскольку путем операций дифференцирования и интегрирования соответствующие результаты получаются просто и естественным образом.

Вернемся к рассматриваемому примеру.

Итак, общее решение в параметрической форме имеет вид

.

Здесь параметр p легко можно исключить. Из первого уравнения находим . Затем подставляя во второе, окончательно получим решение в явном виде

.

3. Уравнение Лагранжа.

Уравнение вида

,

где - данные дифференцируемые функции производной , называется уравнением Лагранжа. В уравнении Лагранжа переменная y является линейной функцией от x с коэффициентами, зависящими от .

Полагая , уравнение Лагранжа сводится к интегрированию линейного уравнения. Кроме того, уравнение Лагранжа может иметь особые решения. Если уравнение имеет вещественные корни , то, кроме того, такие получим решения

,

уравнения Лагранжа. Среди них могут быть особые решения. Геометрически особые решения уравнения Лагранжа представляют прямые.

Рассмотрим пример. Найти решения уравнения

.

Положим . Тогда . Дифференцируя по , получим

.

Отсюда . Сразу же найдем решения, отвечающие корням уравнения . Для p = 0 имеем решение y = 0, а для p = 1, будем иметь y = x – 1.

Далее уравнение запишем в виде

.

Имеем линейное уравнение, кроме того, также является уравнением с разделяющимися переменными. Интегрируя, находим

.

Итак, общий интеграл в параметрической форме записывается так

или .

Исключив параметр , общее решение запишется

. Решение y = 0 является особым, поскольку оно не выделяется из общего решения. Функция y = x – 1 является частным решением, так как она выделяется из общего решения при C = 0.

4. Уравнение Клеро.

Если в уравнении Лагранжа положить 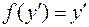, то оно принимает вид

.

Такое уравнение называется уравнением Клеро. При этом функция полагается дважды непрерывно дифференцируемой. Если в уравнении Клеро подставить С вместо , то получим общее решение уравнения Клеро

.

Особая интегральная кривая, как огибающая семейства интегральных кривых определяется в параметрической форме так

.

Таким образом, общее решение уравнения Клеро геометрически представляет собой семейство прямых на координатной плоскости, а особое решение – огибающую этого семейства.

Далее решим следующее уравнение

.

Имеем уравнение Клеро. Общее решение получаем, заменяя в нем на С:

.

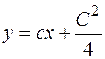Особое решение определяется из системы

,

где второе уравнение получено из первого путем дифференцирования по С. Исключив из системы параметр С, получим особое решение .

Итак, особое решение геометрически представляет параболу, а общее решение – касательные к этой параболе.

Date: 2016-07-25; view: 352; Нарушение авторских прав