Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?
Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника
Уравнения с разделяющимися переменными
|
|
Уравнения вида
P (x) Q (y) d x + M (x) N (y) d y = 0, (5)
в котором коэффициенты при d x и d y являются произведениями функций, зависящих только от одной из переменных x и y, называется уравнением с разделяющимися переменными. Путем деления на M (x) Q (y) приводится к уравнению
(6)
к уравнению с разделенными переменными. Общий интеграл уравнения (5) выражается соотношением
, 
(7)
где С - произвольная постоянная. Если уравнения M (x) = 0 и
Q (y) = 0 имеют вещественные решения x = а, y = b, то функции
x = а, y = b, будучи всегда решениями уравнения (5), могут оказаться, что они выражают решения исходного уравнения, не содержащиеся в общем интеграле (7), так как уравнение (6) было получено из (5) делением на функции M (x) и Q (y).
Поэтому, получив общий интеграл уравнения путем разделения переменных, следует проверить, входят ли в его состав упомянутые частные решения при подходящих числовых значениях параметра С. Если не входят, то их следует записать в ответе отдельно. То есть, в результате разделения переменных могут быть потеряны решения уравнения. (Здесь будьте осторожными!). Вообще, при решении дифференциальных уравнений следует быть очень внимательными. Иногда, наоборот, в результате преобразований над уравнениями могут появиться посторонние решения. Одним словом, четко следите за эквивалентностью цепочки преобразований дифференциальных уравнений или если же решаете не обращая на эквивалентность, то есть, заменяя уравнениями (следствиями), имеющими более широкие множества решений чем исходное, то следует отбрасывать, появившиеся лишние решения.
Задача 1. Решить уравнение
x y d x + (x + 1) d y = 0.
Разделяем переменные
Интегрируем
Для упрощения записи мы обозначили произвольную постоянную не через С, а через ln 
, так как ln может принимать любое действительное значение.
Или
x - ln 
Потенцируя, находим
y = C (x + 1) e 
. (8)
При делении на (x + 1) y могли быть потеряны решения x = -1 и y = 0. Заметим, что решение y = 0 может быть выделено из (8) при С = 0. Решение x = -1 не содержится в (8).
Ответ: y = C (x + 1) e , x = - 1.
2. Линейные уравнения
Уравнения вида
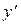+ P (x) y = f (x),
где P (x) и f (x) - непрерывные функции, называется линейным дифференциальным уравнением первого порядка. То есть, неизвестная функция y и ее производная 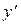входят в уравнение линейно.
Если f (x)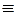 
0, то уравнение называется линейным однородным уравнением первого порядка. 
Проиллюстрируем на примерах, как же интегрируются линейные уравнения.
Задача 2. Решить уравнение
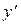+ 2 xy = x e 
.
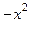Заметим, что уравнение линейное.
1) Метод подстановки.
Положим y = u v. Откуда находим
Подставив в данное уравнение, получим
.
Сгруппируем
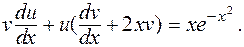(9)
Функцию V определим так, чтобы сумма в скобках обратилась в нуль. Для этого интегрируем уравнение с разделяющимися переменными
Разделяем переменные
Интегрируем
Возьмем частное решение при 
: 
Подставляя функцию 
в левую часть уравнения (9), получаем снова уравнение с разделяющимися переменными относительно функции U = U (x):
Отсюда U = 
Перемножая найденные функции V (x) и U (x, С), находим общее решение исходного уравнения
2) Метод вариации произвольной постоянной.
Сначала находим общее решение линейного однородного уравнения
Имеем уравнение с разделяющимися переменными. Разделяя переменные и интегрируя, получаем
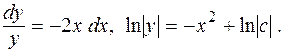
Или
(10)
Далее, найдем общее решение исходного уравнения в виде (10), при этом С будем считать не постоянной, а неизвестной функцией от 
, то есть
Дифференцируя, имеем
Подставляя в данное уравнение выражения для 
, получаем
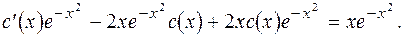
Или
откуда
где 
- произвольная постоянная.
Следовательно, общее решение данного уравнения имеет вид
Замечание. Может случиться следующее: уравнение не оказалось линейным относительно 
и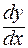 
, однако оно линейное относительно 
и .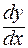
В частности, уравнение
не является линейным относительно и 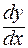, но линейное относительно и 
. Убедимся в этом, представив уравнение в виде
Если же будем решать первым методом, то следует использовать подстановку 
В качестве упражнения самостоятельно решите это уравнение.
Ответ: 
3. Уравнение Бернулли.
Уравнением Бернулли называется уравнение вида
где 
(при 
является линейным, а при 
- уравнением с разделяющимися переменными). Оно сводится к линейному подстановкой 
или можно интегрировать также как и линейное уравнение подстановкой 
Задача 3. Решить уравнение
Имеем уравнение Бернулли. Положим 
отсюда
Подставляя в уравнение, получаем
(11)
Решая уравнение
находим частное решение 
Подставив 
в (11), будем иметь
. 
Интегрируем
Кроме того, u = 0 – решение промежуточного уравнения .
Подставляя, получим общее решение
.
Заметим, что u = 0 соответствует решение 
данного уравнения, которое не выделяется из общего решения.
Замечание: При m > 1 в уравнении Бернулли, - решение этого уравнения.
Решим этот же пример подстановкой . В нашем примере m = 2. Тогда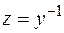 
, 
. В новых обозначениях уравнение примет вид 
. Решая это линейное уравнение, находим 
. Переходя к переменной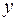 
, получаем общее решение . Кроме того, добавим решение .
Отметим следующее: может получиться, что уравнение является уравнением Бернулли относительно 
В частности, уравнение
не является уравнением Бернулли относительно 
Представив в виде
убеждаемся, что является уравнением Бернулли относительно 
Решить самостоятельно.
Ответ: 
Date: 2016-07-25; view: 416; Нарушение авторских прав