Подставляя найденные значения в формулу (5), получим

Ответ: 2,95.

Остановимся на дифференцировании сложной функции. Пусть z = f (x, y)- функция двух переменных x и у, каждая из которых в свою очередь является функцией независимой переменной t: x = x (t), y = y (t). Тогда функция z =

f (x (t), y (t)) является сложной от t, а x и у - промежуточными переменными.

Пусть функции x = x (t) и y = y (t) дифференцируемы в точке t, а функция z = f (x, y) дифференцируема в точке M (x (t), y (t)). Тогда производная сложной функции вычисляется по формуле:

(6)

В частности, если t совпадает с одним из аргументов, например, с переменной x, то полная производная функции z по x запишется

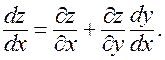(7)

Задача 7. а) Дана сложная функция

где x = ln t, y = sin t.

Найти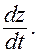

Решение. По формуле (6) получим

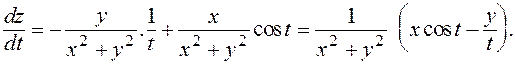
Далее подставляя вместо x и у соответствующие выражения через переменную t, окончательно получим

Замечание. С другой стороны можно найти, предварительно выразив z через t. В самом деле:

б) Найти полную производную если где

Решение. Сначала находим

Затем по формуле (7) получим

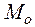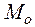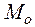Далее рассмотрим задачу на касательную плоскость и нормаль. Предварительно напомним, что плоскость, проходящая через точку поверхности, называется касательной плоскостью к поверхности в этой точке, если угол между секущей, проходящей через точку и любую точку поверхности, и плоскостью стремится к нулю, когда точка стремится к точке . Прямая, проходящая через точку 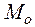ортогонально касательной плоскости, называется нормалью к поверхности в точке .

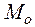Пусть дана поверхность уравнением F (x, y,z) = 0. Предположим, что в точке этой поверхности функции F(x, y,z) дифференцируема. Тогда уравнение касательной плоскости в точке 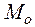к данной поверхности определяется уравнением:

(8)

Уравнение нормали в точке 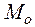имеет следующий вид:

(9)

Пусть уравнение поверхности задано в явной форме z = f (x, y), если f (x, y) дифференцируема в точке , то уравнение касательной плоскости в этой точке запишется

,

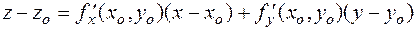где Уравнение нормали имеет вид

Задача 8. Написать уравнения касательной плоскости и нормали к поверхности

в ее точке

Решение.

Находим частные производные и их значения в точке

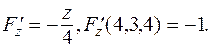
Date: 2016-07-25; view: 475; Нарушение авторских прав