
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Далее, используя уравнения (8) и (9) , получим
|
|
 или 3 x - 4 y – 6 z = 0 - уравнение касательной плоскости;
или 3 x - 4 y – 6 z = 0 - уравнение касательной плоскости;
или  - уравнение нормали.
- уравнение нормали.
Рассмотрим задачи, связанные с нахождением производной по направлению и градиента скалярного поля.
Сначала напомним понятие производной по направлению. Говорят, что в области 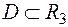 задано скалярное поле, если в ней задана скалярная функция U = U (x, y, z). Иногда под переменными x, y, z удобно понимать координаты радиуса-вектора
задано скалярное поле, если в ней задана скалярная функция U = U (x, y, z). Иногда под переменными x, y, z удобно понимать координаты радиуса-вектора 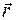 переменной точки
переменной точки  и при этом пишут
и при этом пишут 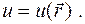
Пусть  - радиус-вектор точки
- радиус-вектор точки 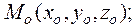 а
а 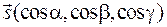 - произвольный единичный вектор,
- произвольный единичный вектор, 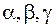 означают углы между вектором
означают углы между вектором  и соответствующими координатными осями. Если существует конечный предел
и соответствующими координатными осями. Если существует конечный предел
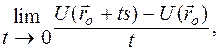
то этот предел называется производной по направлению вектора  в точке
в точке 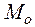 и обозначается
и обозначается 
Если функция U=U (x,y,z) дифференцируемая в точке 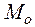 , то для нее производная по направлению
, то для нее производная по направлению  в этой точке вычисляется по формуле:
в этой точке вычисляется по формуле:

 (10)
(10)
Производная в данном направлении характеризует скорость изменения функции в этом направлении.
Как видно из формулы (10), что частные производные 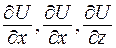
являются производными по направлениям координатных осей. В самом деле, если, в частности, 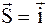 , то
, то 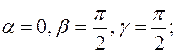 тогда по формуле (10) будем иметь
тогда по формуле (10) будем иметь 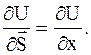
Градиент скалярного поля U = U (x, y, z) в точке M(x, y, z) определяется как вектор, координаты которого равны соответственно частным производным
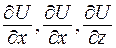 в этой точке, то есть
в этой точке, то есть
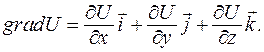
Задача 9. Найти производную функции  в
в
точке 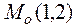 по направлению вектора
по направлению вектора  и grad в точке
и grad в точке 
Решение. Находим частные производные
        
|
| у |
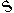
|
| b |
| a |
| М 0(1,2) |
| x |
| 0 |
| Рис. 3 |
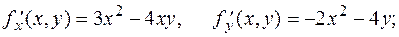
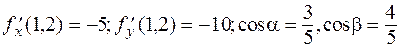 (См. Рис. 3).
(См. Рис. 3).
Итак, 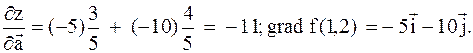

|
| у |
| 0 |
| М 1 |
| x |
| - 4 |
| - 4 |
| М 2 |
Рис. 4
Задача 10. Найти наибольшее и наименьшее значения функции
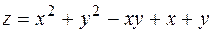 в треугольнике, ограниченными прямыми x = 0, y = 0, x + y = -4 (См. рис. 4).
в треугольнике, ограниченными прямыми x = 0, y = 0, x + y = -4 (См. рис. 4).
Напомним, что функция f (x, y), дифференцируемая в ограниченной замкнутой области, достигает своего наибольшего (наименьшего) значения или в стационарной точке или в граничной точке области.
1. Найдем стационарные точки, лежащие внутри данного треугольника:
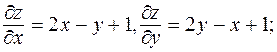
Решая систему
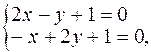
находим стационарную точку  , которая лежит внутри треугольни-
, которая лежит внутри треугольни-
ка. Значение функции в этой точке 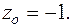
2. Исследуем функцию на границе области. Для этого рассмотрим функцию отдельно на каждой стороне треугольника.
а) Исследование на стороне  треугольника. На этой стороне y = 0, поэтому
треугольника. На этой стороне y = 0, поэтому  Задача сводится к отысканию наибольшего и наименьшего значений этой функции одной переменной на отрезке
Задача сводится к отысканию наибольшего и наименьшего значений этой функции одной переменной на отрезке 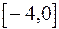 . На концах этого отрезка Z (-4) = 12; Z (0) = 0. Найдем стационарные точки из уравнения
. На концах этого отрезка Z (-4) = 12; Z (0) = 0. Найдем стационарные точки из уравнения  .
.
При этом 
Итак,  в точке
в точке  в точке
в точке 
б) Исследование на стороне  треугольника. На этой стороне x = 0,
треугольника. На этой стороне x = 0,
тем самым  Аналогично получим
Аналогично получим  в точке
в точке  в точке
в точке 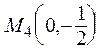 .
.
в) Исследование на стороне  . На этой стороне y = - x -4
. На этой стороне y = - x -4  Тогда получим
Тогда получим 
 На концах отрезка Z (-4) = 12, Z (0) = 12. Найдем стационарную точку:
На концах отрезка Z (-4) = 12, Z (0) = 12. Найдем стационарную точку: 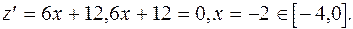
Итак,  в точках
в точках 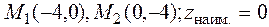 в точке
в точке 
3. Сопоставляя все полученные значения функции, заключаем, что  в точках
в точках 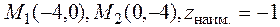 в стационарной точке
в стационарной точке 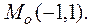
Date: 2016-07-25; view: 374; Нарушение авторских прав

