Краткие теоретические сведения и упражнения

Теперь изложим методы решения ряда типовых задач, разбор которых окажет студенту-заочнику существенную методическую помощь при выполнении настоящей контрольной работы.

Сначала напомним, что под областью определения функции z = f (x, y) будем понимать совокупность точек плоскости Oxy, в которых данная функция определена, то есть, принимает определенные действительные значения.

Задача 1. Найти области определения следующих функций:

Решение. a) Областью определения данной функции является множество всех точек М (x, y), для которых выражение определено; то есть совокупность точек M (x, y), для которых или Кроме того, еще можно записать так: . Область определения D образует круг с центром в начале координат и радиусом, равным 3. При этом окружность не входит в область D (см. Рис. 1.).

б) Данная функция определена только для таких точек M (x, y), координаты которых удовлетворяют системе неравенств

То есть, область определения

Для того чтобы уяснить, где расположены на плоскости точки, координаты которых удовлетворяют неравенству Y <3- X, рассмотрим прямую: Y =3- X. Множество точек M (x, y), удовлетворяющих неравенству Y <3- X, есть часть плоскости Ox y, расположенная ниже прямой Y =3- X. Заметим, что совокупность точек , координаты которых удовлетворяют неравенству

есть множество точек, расположенных в первой и третьей четвертях;

кроме того, этому условию удовлетворяют точки, лежащие на координатных осях. Пересечение двух множеств и 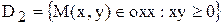дает область определения рассматриваемой функции, то есть , ее геометрическое изображение дано на Рис 2. При этом точки отрезка не входят в область определения.

y y 3 M 2 M 1 3 x 0 3 x

Прежде чем приступить к рассмотрению следующей задачи вспомним ряд понятий и определений.

Пусть функция z = f (x, y) определена в некоторой окрестности точки M (x, y). Придадим переменной x в точке М произвольное приращение D x, оставляя значение переменной y неизменным. При этом D x таково, что точка x+Dx, y лежит в указанной окрестности точки М. Тогда D Z= f (x +D x, y) - f (x, y) называется частным приращением функции по переменной x в точке M (x, y).

Аналогично определяется частное приращение функции по переменной y.

Определение. Если существует конечный предел , то он называется частной производной функции z = f (x, y) в точке M (x, y) по переменной x и обозначается одним из следующих символов: Точно также определяется частная производная по переменной y.

Если нужно явно указать, в какой точке вычислена та или другая частная производная, то пишут так:

или или .

Из определения следует, что частная производная функции двух переменных z = f (x, y) по переменной x представляет собой обыкновенную производную функции одной переменной x при фиксированном значении переменной y. Поэтому частные производные вычисляют по формулам и правилам вычисления производных функций одной переменной.

Понятие частной производной определяется так же и для функций любого

числа переменных. Так, для функции трех переменных U(x, y, z) можно опре-

делить три частные производные:

.

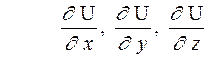Задача 2. Найти частные производные следующих функций

Решение.

а)

б)

в)

Можно ввести понятие частной производной порядка выше первого. Пусть частные производные функции z = f (x, y), определенной в окрестности точки M (x, y), существует в каждой точке этой окрестности. Тогда рассматриваемые частные производные представляют собой функции двух переменных x и y в окрестности точки М. Назовем их частными производными первого порядка. В свою очередь можно рассматривать частные производные по переменным x и y функций в точке M(x, y); если они существуют, то называются частными производными второго порядка функции z = f (x, y) в этой точке и обозначаются следующими соответствующими символами:

Частные производные второго порядка

называются смешанными частными производными.

Задача 3. Дана функция

Найти

Решение. Находим

Заметим, что смешанные производные и 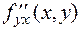равны. Но, вообще говоря, значения смешанных частных производных зависят от порядка, в котором производится дифференцирование.

В связи с этим сформулируем утверждение, которое гарантирует равенство смешанных производных:

если смешанные производные существуют в некоторой окрестности точки и непрерывны в самой точке 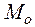, то они равны в этой точке; то есть

Можно определить частные производные еще более высоких порядков:

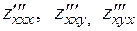и т.д.

Задача 4. Дана функция Показать, что

(1)

Решение. Находим последовательно необходимые частные производные второго порядка данной функции:

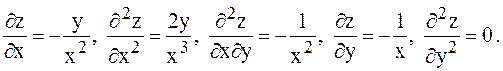
Подставляя в левую часть (1), получим:

Следовательно, функция действительно удовлетворяет (1).

Теперь рассмотрим понятие дифференцируемости функции. Прежде всего, напомним, что полным приращением функции Z = f (x, y) в точке M (x, y), соответствующим приращениям переменных x и y, называется разность . При этом предполагается, что функция определена в некоторой окрестности точки М (x,у).

Функция z = f (x, y) называется дифференцируемой в точке М (x,у), если ее полное приращение в этой точке может быть представлено в виде

(2)

где A и B - некоторые независимые от и 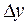числа, а и 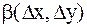- бесконечно малые при функции, то есть и при и Полным дифференциалом функции z = f (x, y) в точке М (x,у) называется главная часть полного приращения этой функции в рассматриваемой точке, линейная относительно и 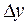, то есть

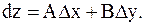
Дифференциалами независимых переменных x и у назовем приращения этих переменных: Для дифференциала функции z = f (x, y) справедлива формула:

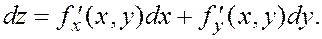(3)

Для функций многих переменных остаются справедливыми следующие правила:

.

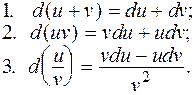Из и следует, что разность между полным приращением и диф-

ференциалом функции в точке М (x,у) есть бесконечно

малая при более высокого порядка, чем , где - расстояние между точками М (x,у) и Тем самым при достаточно малых и 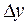получаем

приближенную формулу которую широко используют в приближенных вычислениях. Эту приближенную формулу перепишем в виде

(4)

Теперь рассмотрим примеры.

Задача 5. Найти дифференциал функции

Решение. 1-й способ. Используем выше указанные правила (1-3)

2-й способ. Воспользуемся формулой (3). Для этого находим частные производные:

Наконец, по формуле (3) получаем

Задача 6. Пользуясь формулой (4), вычислить приближенно

Решение. Искомое число будем рассматривать как значение функции в точке Формулу (4) перепишем так

(5)

где В качестве и 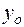возьмем соответственно числа 1 и 2. Следовательно,

Имеем 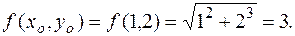Находим:

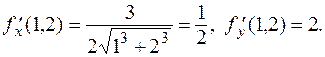
Date: 2016-07-25; view: 351; Нарушение авторских прав