Геометрическое место точек. Круг и окружность

Геометрическое место точек. Срединный перпендикуляр. Биссектриса угла.

Окружность. Круг. Центр окружности. Радиус. Дуга. Секущая. Хорда.

Диаметр. Касательная и её свойства. Сегмент. Сектор. Углы в круге.

Длина дуги. Радиан. Соотношения между элементами круга.

Геометрическое место точек – это множество всех точек,удовлетворяющих определённым заданным условиям.

П р и м е р 1. Срединный перпендикуляр любого отрезка есть геометрическое

место точек (т.е. множество всех точек), равноудалённых от

концов этого отрезка. Пусть PO 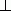AB и AO = OB:

Тогда, расстояния от любой точки P, лежащей на срединном перпендикуляре PO, до концов A и B отрезка AB одинаковы и равны d.

Таким образом, каждая точка срединного перпендикуляра отрезка обладает следующим свойством: она равноудалена от концов отрезка.

П р и м е р 2. Биссектриса угла есть геометрическое место точек, равноудалённых от его сторон.

П р и м е р 3. Окружность есть геометрическое место точек (т.е. множество

всех точек), равноудалённых от её центра (на рис. показана одна

из этих точек – А).

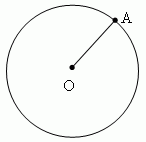
Окружность - это геометрическое место точек (т.е. множество всех точек) на плоскости, равноудалённых от одной точки, называемой центром окружности. Отрезок, соединяющий центр окружности с какой-либо её точкой, называется радиусом и обозначается r или R. Часть плоскости, ограниченная окружностью, называется кругом. Частьокружности(A m B, рис.39) называется дугой. Прямая PQ, проходящая через точки M и N окружности (рис.39), называется секущей, а её отрезокMN, лежащий внутри окружности - хордой.

Хорда, проходящая через центр круга (например, BC, рис.39), называется диаметром и обозначается d или D. Диаметр – это наибольшая хорда, равная двум радиусам (d =2 r).

Касательная. Предположим, секущая PQ (рис.40) проходит через точкиK и M окружности. Предположим также, что точка M движется вдоль окружности, приближаясь к точке K. Тогда секущая PQ будет менять своё положение, вращаясь вокруг точки K. По мере приближения точки M к точке K секущая PQ будет стремиться к некоторому предельному положению АВ. Прямая AB называется касательной к окружности в точке K. Точка K называется точкой касания. Касательная и окружность имеют только одну общую точку – точку касания.

Date: 2016-11-17; view: 730; Нарушение авторских прав