Площади плоских фигур

Площади плоских фигур: квадрат, прямоугольник, ромб,

параллелограмм, трапеция, четырёхугольник,

прямоугольный треугольник, равнобедренный треугольник,
равносторонний треугольник, произвольный треугольник,

многоугольник, правильный шестиугольник,
круг, сектор, сегмент круга. Формула Герона.

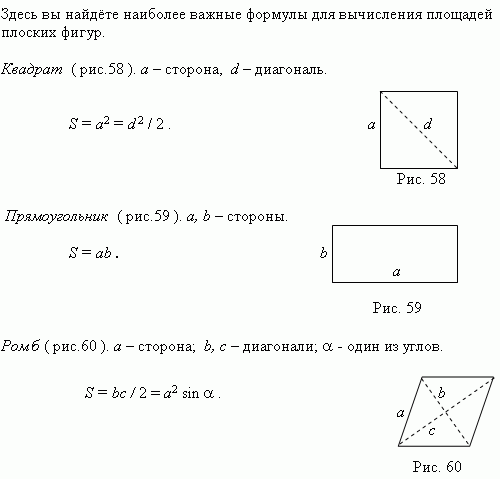
Произвольный треугольник. a, b, c – стороны; a – основание; h – высота;

A, B, C – углы, противоположные сторонам a, b, c; p = (a + b + c) / 2.

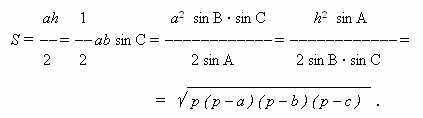
Последнее выражение называется формулой Герона.

Многоугольник, площадь которого нужно определить,может быть разделён своими диагоналями на несколько треугольников. Многоугольник, описанный около круга (рис.67), может быть разделён прямыми, идущими из центра круга к его вершинам. Тогда получаем:

В частности, эта формула справедлива для любого правильного многоугольника.

Правильный шестиугольник. a – сторона.

Круг. D – диаметр; r – радиус.

Сектор (рис.68). r – радиус; n – величина центрального угла в градусах; l –длина дуги.

Сегмент (рис.68).Площадь сегмента определяется как разность междуплощадями сектора A m BO и треугольника AOB. Кроме того, есть приближённая формула для площади сегмента:

где a = AB (рис.68) – основание сегмента; h – его высота (h = r – OD). Относительная погрешность этой формулы: при A m B = 60° – около 1.5%; при A m B = 30° - ~ 0.3%.

П р и м е р. Вычислить площади сектора A m BO (рис.68) и сегмента A m B

при следующих данных: r = 10 см, n = 60°.

Р е ш е н и е. Площадь сектора:

Площадь правильного треугольника AOB:

Отсюда, площадь сегмента:

S = S ₁ – S ₂ = 52.36 – 43.30 = 9.06 см ² .

Заметим, что в правильном треугольнике AOB:

AB = AO = BO = r, AD = BD = r / 2, и поэтому высота OD

в соответствии с теоремой Пифагора равна:

Тогда, по приближённой формуле получим: