Пример выполнения заданий по теме 6

Задание 6.1. Решить дифференциальное уравнение первого порядка.

а) ;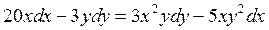

б) ;

в) .

Решение.

а) Уравнение 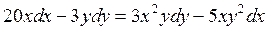является уравнением с разделяющимися переменными.

1. Разделим переменные. Перенесем слагаемые с dx в левую часть, а слагаемые с dy в правую: . Вынесем за скобки общие множители: 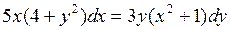. Разделим обе части на (4 + y )·(x + 1): .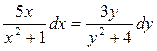

2. Возьмем интегралы от правой и левой частей уравнения, применив метод подстановки:

, =

= . Аналогично .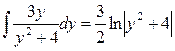

Тогда: 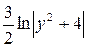= , здесь .

3. Выразим y из данного равенства. Для этого умножим данное равенство на 2 и применив свойства логарифмов, получим: .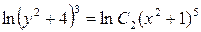

Откуда Здесь . Таким образом, y = .

б) Уравнение является линейным уравнением. Разделим обе части на x. Тогда получим: y' + = 1 + .

Решим данное уравнение методом Бернулли. Решение уравнения ищем в виде y = uv, тогда y' = u'v + uv'. Подставим y' и y в уравнение y' + = 1 + y' + = 1 + . Тогда получим:

u'v + uv' + 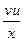= 1 + . Сгруппируем второе и третье слагаемое левой части уравнения и вынесем за скобки u, тогда получим u'v + u (v' + ) = 1 + .

1. Найдем частное решение уравнения v' + = 0. Это уравнение с разделяющимися переменными. Заменим v' на и разделим переменные v и x: . Тогда и . Откуда по свойствам логарифмов получаем v = 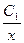. Возьмем C = 1 и получим искомое частное решение: v = .

2. Подставим данное частное решение в уравнение u'v + u (v' + ) = 1 + . Тогда получим u'· = 1 + , которое является уравнением с разделяющимися переменными. Найдем общее решение данного уравнения. Так как u' = то имеем . Умножим обе части данного уравнения на dx·x, получим du = (x + 1) dx. Взяв интегралы от обеих частей уравнения: , получим u = 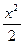+ x + C.

3. Тогда y = uv = (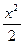 + x + C)· = .

в) Разделим обе части уравнения на y, тогда получим , которое является однородным дифференциальным уравнением первого порядка, так как .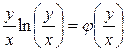

Введем новую переменную u = 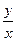и найдем y' = u'x + u. Подставим y' и y в уравнение , которое будет уравнением с разделяющимися переменными: u'x + u = u·lnu. Разделим переменные u и x. Так как u' = то имеем . Умножим обе части уравнения на . В итоге получим .

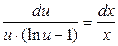Возьмем интегралы от обеих частей уравнения. Так как , то имеем: 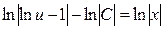. Перенесем в правую часть уравнения и применив свойства логарифмов (учитывая, что С – константа), получим lnu – 1 = C x, откуда lnu = Cx + 1. Тогда u = e 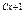. Так как y = ux, то получаем: y = x·e .

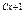Ответ: а) y = ; б) y = ; в) y = x·e .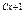

Задание 6.2. Решить уравнения:

а)

б)

в)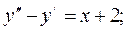

г)

Решение.

а) Общее решение данного линейного уравнения второго порядка с постоянными коэффициентами найдем, как сумму общего решения соответствующего однородного уравнения и частного решения исходного неоднородного уравнения:

1. Найдем общее решение однородного уравнения Для этого составим характеристическое уравнение для данного линейного однородного дифференциального уравнения: Найдем корни этого квадратного уравнения: Так как в случае D = 0 общее решение линейного однородного дифференциального второго порядка с постоянными коэффициентами имеет вид 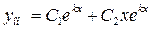, то общее решение исходного уравнения будет иметь вид:

2. Теперь найдем частное решение исходного дифференциального уравнения

. Так как f (x) = , то частное решение данного дифференциального уравнения имеет вид:

= y = .

Для нахождения A воспользуемся методом неопределенных коэффициентов.

Подставляя в исходное уравнение , получаем:

Откуда

Частное решение имеет вид: =

3. Тогда общее решение линейного неоднородного уравнения будет иметь вид:

б) Общее решение данного линейного уравнения второго порядка с постоянными коэффициентами найдем, как сумму общего решения соответствующего однородного уравнения и частного решения исходного неоднородного уравнения:

1. Найдем общее решение однородного уравнения 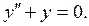Для этого составим характеристическое уравнение для данного линейного однородного дифференциального уравнения: Найдем корни этого квадратного уравнения: i. Так как в случае D < 0 общее решение линейного однородного дифференциального второго порядка с постоянными коэффициентами имеет вид , то общее решение исходного уравнения будет иметь вид: .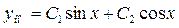

2. Теперь найдем частное решение исходного дифференциального уравнения

. Так как f (x) = , то частное решение данного дифференциального уравнения имеет вид:

= y = .

Для нахождения A и B воспользуемся методом неопределенных коэффициентов.

Приведя подобные слагаемые в левой части уравнения, получим:

.

Откуда

Тогда = y = .

3. Тогда общее решение линейного неоднородного уравнения будет иметь вид:

в) Общее решение данного линейного уравнения второго порядка с постоянными коэффициентами найдем, как сумму общего решения соответствующего однородного уравнения и частного решения исходного неоднородного уравнения:

1. Найдем общее решение однородного уравнения Для этого составим характеристическое уравнение для данного линейного однородного дифференциального уравнения: Найдем корни этого квадратного уравнения: Так как в случае D >0 общее решение линейного однородного дифференциального второго порядка с постоянными коэффициентами имеет вид , то общее решение исходного уравнения будет иметь вид:

2. Теперь найдем частное решение исходного дифференциального уравнения

. Так как f (x) = , то частное решение данного дифференциального уравнения имеет вид:

= y = .

Для нахождения A и B воспользуемся методом неопределенных коэффициентов.

Подставляя в исходное уравнение , получаем:

2 A – 2 Ax – B = x + 2. Приравнивая коэффициенты при и , получим:

: – 2 Ax = 1;

: 2 A – B = 2. Откуда находим: A = , B = – 3.

Тогда частное решение имеет вид: =

3. Тогда общее решение линейного неоднородного уравнения будет иметь вид:

г) Общее решение данного линейного уравнения второго порядка с постоянными коэффициентами найдем, как сумму общего решения соответствующего однородного уравнения и частного решения исходного неоднородного уравнения:

1. Найдем общее решение однородного уравнения Для этого составим характеристическое уравнение для данного линейного однородного дифференциального уравнения: Найдем корни этого квадратного уравнения: Так как в случае D > 0 общее решение линейного однородного дифференциального второго порядка с постоянными коэффициентами имеет вид , то общее решение исходного уравнения будет иметь вид:

2. Теперь найдем частное решение исходного дифференциального уравнения

Так как f (x) = , то частное решение данного дифференциального уравнения имеет вид:

= y = .

Для нахождения A и B воспользуемся методом неопределенных коэффициентов.

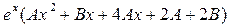= . Подставляя в исходное уравнение , получаем: - 7 +

+ 6 = . Вынесем в левой части уравнения за скобки, разделим обе части уравнения на и уравняем коэффициенты при , и . Тогда получим:

: A - 7 A + 6 A = 0,

: B + 4 A – 7 B – 14 A + 6 B = 1,

: 2 A + 2 B – 7 B = – 2.

После упрощений получаем:

: 0 = 0,

: – 10 A = 1, откуда A = - 0,1.

: 2 A – 5 B = – 2. Подставляя вместо A = - 0,1, получим B = 0,36.

Таким образом, частное решение имеет вид: =

3. Тогда общее решение линейного неоднородного уравнения будет иметь вид:

Тема 7. Ряды.

Date: 2016-11-17; view: 303; Нарушение авторских прав