Пример выполнения заданий по теме 7

Задание 7.1. Исследовать сходимость ряда.

а) ; б) ; в) ; г) ;

д) ; е) ; ж) ; з) .

Решение.

а) Так как для любого натурального n, а ряд 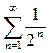сходится, как ряд геометрической прогрессии с q = < 1, то и ряд тоже сходится по первому признаку сходимости знакоположительных рядов.

б) При n > 1 ln n < n, поэтому . Гармонический ряд расходится, поэтому по свойствам числовых рядов расходится и ряд . Тогда по первому признаку сравнения знакоположительных рядов расходится и ряд .

в) У данного ряда общий член Найдем . Тогда по признаку Даламбера ряд сходится.

г) Воспользуемся признаком Даламбера.

, . Тогда =

= > 1, то есть по признаку Даламбера ряд расходится.

д) У данного ряда u = . Применим радикальный признак Коши и найдем . Значит, исходный ряд сходится.

е) Применим необходимый признак сходимости:

, поэтому данный ряд расходится.

ж) Исследуем сходимость ряда с помощью интегрального признака Коши. Рассмотрим функцию , при она является непрерывной, положительной и убывающей.

Исследуем сходимость несобственного интеграла

Найдем сначала = .

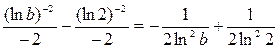Вычислим

Таким образом, несобственный интеграл сходится, значит и ряд сходится.

з) У данного ряда общий член ряда . Составим вспомогательный ряд с . Ряд является рядом Дирихле , который при = 3 > 1 сходится. Найдем

= 1. Так как 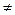1 0 и 1 , то по второму (предельному) признаку сходимости рядов ряды и ведут себя одинаково, а так как ряд сходится, то и ряд также сходится.

Задание 7.2. Найти область сходимости степенного ряда.

а) 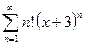; б) ; в) .

Решение.

а) Радиус сходимости данного степенного ряда R найдем по формуле

R = .

Так как a = n!, a = (n + 1)!, то R = = 0.

Поэтому область сходимости данного степенного ряда будет состоять из одного числа: x {-3}.

б) Так как a = , a = , то R = = = = 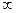. Поэтому область сходимости степенного ряда будет множество всех действительных чисел: x (- : + ).

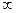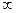в) 1. У данного степенного ряда a = , a = . Найдем радиус сходимости данного степенного ряда:

R = = = 3.

2. Найдем интервал сходимости данного степенного ряда: 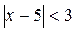. Таким образом, интервал сходимости данного ряда (2; 8).

3. Исследуем сходимость степенного ряда на концах интервала.

а) При x = 8 получим числовой ряд = = 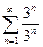. Так как = 1 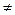0, то по необходимому признаку сходимости числовых рядов получившийся числовой ряд расходится, поэтому число x = 8 не входит в область сходимости степенного ряда.

б) При x = 2 получим числовой ряд = = = . Так как 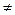0 (данный передел не существует), то по необходимому признаку сходимости числовых рядов получившийся числовой ряд расходится, поэтому число x = 2 не входит в область сходимости степенного ряда.

4. Таким образом, область сходимости данного степенного ряда x (2: 8).

Date: 2016-11-17; view: 302; Нарушение авторских прав