
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Пример выполнения заданий по теме 4
|
|
Задание 4.1. Найти производные 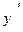 данных функций.
данных функций.
а) 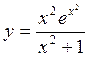 ; б)
; б) 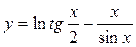
Решение.
а) Для нахождения производной воспользуемся правилом нахождения производной частного 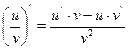 и производной сложной функции:
и производной сложной функции:
y' = 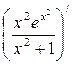 =
= 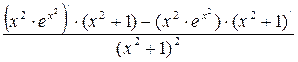 =
=
= 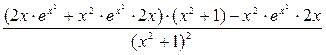 =
=
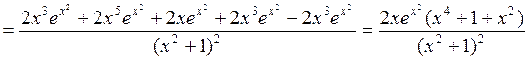 .
.
б) Для нахождения производной функции применим правила нахождения производной разности и производной частного, а также дважды применим правило нахождения производной сложной функции:
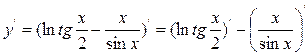 =
= 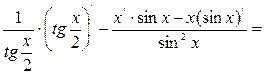
= 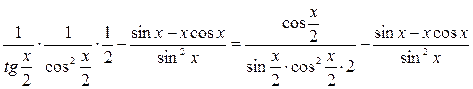 =
=
= 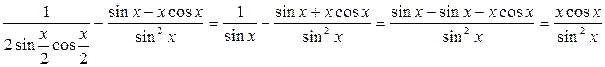
Задание 4.2. Исследовать функцию 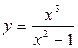 и построить ее график.
и построить ее график.
Решение.
При исследовании функции будем придерживаться следующей схемы:
1. Найдем область определения функции.
2. Найдем точки пересечения графика функции с осями координат.
3. Исследуем функцию на четность и нечетность.
4. Найдем асимптоты графика функции.
5. Найдем y' и с помощью ее определим промежутки возрастания и убывания функции, экстремумы функции.
6. Найдем y'' и с помощью ее определим промежутки выпуклости и вогнутости графика функции и точки перегиба.
7. Используя пункты 1 – 6 данной схемы строим график функции, в случае затруднения берем несколько дополнительных точек.
1. Так как дробь 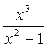 определена при всех значениях x
определена при всех значениях x 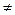
 1, то областью определения функции будет D (f) = (-¥; -1) È (-1; 1) È (1; +¥).
1, то областью определения функции будет D (f) = (-¥; -1) È (-1; 1) È (1; +¥).
2. а) Найдем точки пересечения с осью абсцисс: y = 0, поэтому 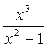 = 0, откуда x = 0. Таким образом, получаем точку пересечения с осью OX: точку O (0; 0).
= 0, откуда x = 0. Таким образом, получаем точку пересечения с осью OX: точку O (0; 0).
б) Найдем точки пересечения с осью ординат: x = 0, тогда y = 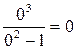 . В итоге получаем ту же точку O (0; 0).
. В итоге получаем ту же точку O (0; 0).
3. Найдем y (- x) = 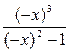 =
= 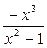 = – y (x), то есть функция
= – y (x), то есть функция 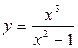 является нечетной.
является нечетной.
4. а) Найдем вертикальные асимптоты графика функции. Найдем 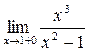 =
=  ,
, 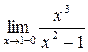 =
= 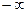 . Значит, прямая x = 1 является вертикальной асимптотой графика функции
. Значит, прямая x = 1 является вертикальной асимптотой графика функции 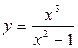 .
.
Найдем  =
= 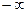 ,
,  =
=  . Значит, прямая x = - 1 является вертикальной асимптотой графика функции
. Значит, прямая x = - 1 является вертикальной асимптотой графика функции 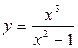 .
.
б) Найдем горизонтальные асимптоты графика функции. Для этого найдем 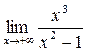 =
= 
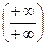 =
= 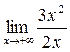 =
= 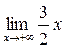 = +
= + 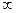 . (При вычислении предела применили правило Лопиталя). Аналогично,
. (При вычислении предела применили правило Лопиталя). Аналогично, 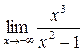 = -
= - 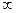 .
.
Таким образом, горизонтальных асимптот график функции не имеет.
в) Найдем наклонные асимптоты графика функции. Так как наклонная асимптота имеет вид y = kx + b, то найдем k и b. k = 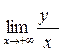 =
= 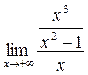 =
= 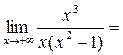
 =
= 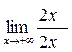 = 1. Аналогично,
= 1. Аналогично, 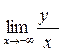 = 1. Таким образом, k = 1. b =
= 1. Таким образом, k = 1. b =  (y – kx) =
(y – kx) = 
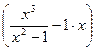 =
= 
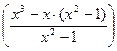 = =
= = 
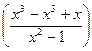 =
= 
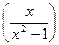 =
= 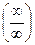 =
= 
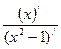 =
= 
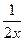 = 0.
= 0.
Значит, график функции имеет наклонную асимптоту y = x.
5. Найдем производную функции 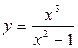 :
:
 =
=  .
.
Решая уравнение  = 0, находим критические точки: x = 0; x = -
= 0, находим критические точки: x = 0; x = - 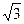 ; x =
; x = 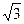 ; x = -1; x = 1.
; x = -1; x = 1.
Найдем промежутки возрастания и убывания функции.
Для этого определяем знаки производной функции на промежутках.
x < - 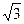 , y ¢ > 0, функция возрастает
, y ¢ > 0, функция возрастает
- 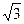 < x < -1, y ¢ < 0, функция убывает
< x < -1, y ¢ < 0, функция убывает
-1 < x < 0, y ¢ < 0, функция убывает
0 < x < 1, y ¢ < 0, функция убывает
1 < x < 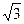 , y ¢ < 0, функция убывает
, y ¢ < 0, функция убывает
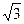 < x, y ¢ > 0, функция возрастает
< x, y ¢ > 0, функция возрастает
Так как при переходе через точку х = - 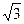 знак производной функции меняется с «плюса» на «минус», то точка х = -
знак производной функции меняется с «плюса» на «минус», то точка х = - 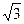 является точкой максимума. А так как при переходе через точку х =
является точкой максимума. А так как при переходе через точку х = 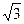 знак производной функции меняется с «минуса» на «плюс», то точка х =
знак производной функции меняется с «минуса» на «плюс», то точка х = 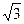 является точкой минимума. Значения функции в этих точках равны: y
является точкой минимума. Значения функции в этих точках равны: y 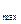 = y (-
= y (- 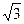 ) = -
) = - 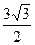
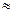 -2,6, y
-2,6, y  = y (
= y (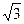 ) =
) = 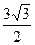
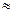 -2,6.
-2,6.
Данные проведенного исследования можно кратко изобразить на следующей схеме:
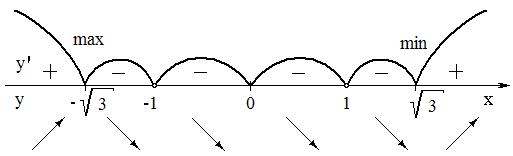
6. Найдем вторую производную функции


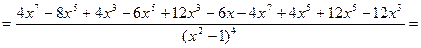
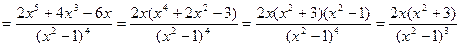 .
.
Определим выпуклость и вогнутость графика функции на промежутках:
x < -1, y ¢¢ < 0, кривая выпуклая
-1 < x < 0, y ¢¢ > 0, кривая вогнутая
0 < x < 1, y ¢¢ < 0, кривая выпуклая
1< x, y ¢¢ > 0, кривая вогнутая
Таким образом, точка O (0; 0) – точка перегиба графика функции.
Данные проведенного исследования можно изобразить схематически:

7. Используя данные проведенного исследования, построим график функции. Для уточнения графика найдем несколько точек графика функции:
| x | 0,5 | ||
| y | 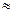 -0,2 -0,2
| 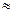 2,7 2,7
| 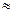 3,4 3,4
|

Date: 2016-11-17; view: 308; Нарушение авторских прав