Краткие теоретические сведения

Выражение 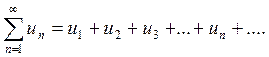называется рядом.

Слагаемые называются членами ряда, 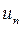- общий член ряда.

Ряд называется числовым, если все его члены являются числами.

Ряд называется функциональным, если все его члены – функции.

Сумма конечного числа первых n членов ряда называется n–й частичной суммой ряда: .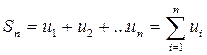

Если существует конечный предел последовательности частич-ных сумм ряда, то ряд называется сходящимся, а число S называется суммой ряда.

Если не существует или равен бесконечности, то ряд называется расходящимся.

Необходимый признак сходимости числового ряда: Если ряд сходится, то .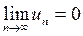

Следствие (достаточный признак расходимости числового ряда): Если 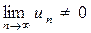или не существует, то числовой ряд расходится.

Ряд 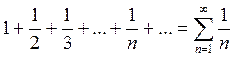называется гармоническим.

Теорема: Гармонический ряд расходится.

Ряд называется знакоположительным (неотрицательным), если для любого натурального n .

Достаточные признаки сходимости знакоположительных рядов:

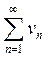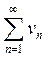Первый признак сравнения: Пусть даны два знакоположительных ряда и , и пусть для любого натурального n выполняется условие: . Тогда, если ряд - сходится, то и ряд сходится; а если ряд расходится, то и ряд 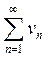расходится.

Второй признак сравнения (предельный): Пусть даны два знакоположительных ряда и 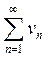, и пусть существует 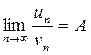, , 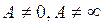тогда оба ряда и 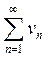одновременно сходятся или расходятся.

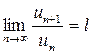Признак Даламбера: Пусть дан знакоположительный ряд и существует предел . Тогда ряд будет сходиться при l < 1 и расходиться при l > 1.

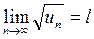Радикальный признак Коши: Пусть дан знакоположительный ряд и существует предел . Тогда ряд будет сходиться при l < 1 и расходиться при l > 1.

Интегральный признак Коши: Если 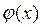- непрерывная положительная функция, убывающая на промежутке [1; + ), то ряд 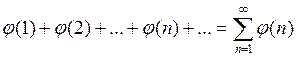и несобственный интеграл 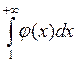одновременно сходятся или расходятся.

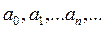Степенным рядом называется функциональный ряд вида , где и 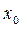- действительные числа.

Множество значений переменной x, при которых соответствующий числовой ряд сходится, называется областью сходимости степенного ряда.

Область сходимости степенного ряда находится по следующему плану:

1. Находится радиус сходимости степенного ряда по формулам: 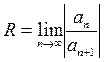или .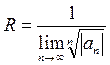

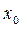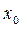2. Записывается интервал сходимости степенного ряда: ( - R; + R).

3. Исследуется сходимость соответствующего числового ряда при значениях x = 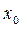- R; x = 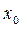+ R.

4. С учетом проведенного исследования записывается область сходимости исходного степенного ряда.

Date: 2016-11-17; view: 291; Нарушение авторских прав