
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Площадь плоской фигуры
|
|
Площадь фигуры, ограниченной графиком непрерывной функции  , двумя прямыми x=a и x=b и осью Ox (такую фигуру называют криволинейной трапецией, Рис. 3.2.) вычисляется по формуле
, двумя прямыми x=a и x=b и осью Ox (такую фигуру называют криволинейной трапецией, Рис. 3.2.) вычисляется по формуле
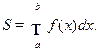
Площадь фигуры, ограниченной графиками непрерывных функций  и двумя прямыми x=a и x=b (Рис. 3.3.), вычисляется по формуле
и двумя прямыми x=a и x=b (Рис. 3.3.), вычисляется по формуле


Рис. 3.2. Рис. 3.3.
Например.


Рис. 3.4.
Если фигура ограничена кривой, имеющей параметрические уравнения x=x(t), y=y(t), прямыми x=a, x=b и осью Ox, то площадь ее вычисляется по формуле

где пределы интегрирования находятся из уравнений a=x(t1), b=x(t2) (y(t)  0 на отрезке [ t1, t2 ]).
0 на отрезке [ t1, t2 ]).
Эта формула применима также для вычисления площади фигуры, ограниченной замкнутой кривой (изменение параметра t от t1 до t2 должно соответствовать обходу контура по часовой стрелке).
Например.


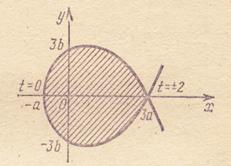
Рис. 3.5.
Площадь фигуры, ограниченной графиком непрерывной функции 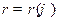 и двумя лучами
и двумя лучами  , где
, где 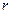 и
и  - полярные координаты, или площадь криволинейного сектора, ограниченного дугой графика функции
- полярные координаты, или площадь криволинейного сектора, ограниченного дугой графика функции  , вычисляется по формуле
, вычисляется по формуле

Например.

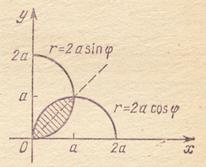
Рис. 3.6.
Длина дуги кривой
Если гладкая кривая задана уравнением y=f(x), то длина l ее дуги равна

где a и b - абсциссы концов дуги.
Если же кривая задана параметрическими уравнениями 

 то
то
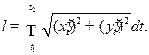
Аналогично выражается длина дуги пространственной кривой, заданной параметрическими уравнениями 

Если задано полярное уравнение гладкой кривой  то
то

Например.



Date: 2016-05-24; view: 437; Нарушение авторских прав