Основные теоремы теории вероятностей. Условная вероятность

Теорема 1. Вероятность суммы двух несовместных событий А и В равна сумме их вероятностей:

Р(А+В)=Р(А)+Р(В).

Следствие 1. Если А ₁, А ₂,..., А_n - попарно несовместные события, то вероятность их суммы равна сумме вероятностей этих событий:

P (A ₁ + А ₂ +... + A_n) = Р (А ₁) + Р (А ₂) +... + Р (А_n).

Следствие 2. Вероятность суммы попарно несовместных событий А ₁, А ₂,..., А_n,образующих полную группу, равна1:

Р (A ₁ + А ₂ +... + A_n)= Р (А ₁) + Р (А ₂) +... + Р (А_n) =1.

Следствие 3. События А и несовместны и образуют полную группу событий, поэтому

.

Отсюда

.

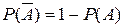Пример 1. В урне 30 шаров, из них 10 – красных, 5 – синих, 15 – белых. Наудачу вынимают один шар. Найти вероятность появления цветного шара.

Решение. Обозначим события: A – появление красного шара, В – появление синего шара.

Число всех исходов n =30, из них благоприятных событию А – десять, а событию В – пять, т.е. , . Нас интересует сумма несовместных событий A + В – появление либо красного, либо синего шара. По теореме сложения вероятностей .

Пример 2. Из полной колоды карт (52 карты) наугад вынимают три карты (без возврата). Найти вероятность того, что среди вынутых карт будет хотя бы один туз.

Решение. Обозначим события:

А – появление одного туза в 3 взятых картах;

В – появление двух тузов;

С – появление трех тузов;

D – среди вынутых карт нет тузов.

Нас интересует сумма несовместных событий (А + В + С) либо один, либо два, либо три туза (хотя бы один). 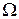состоит из равновозможных исходов, число которых равно числу способов взять 3 карты из 52, т.е. числу сочетаний . Исходы, благоприятные событиям А, В, С, соответственно равны

,

,

,

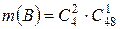Следовательно,

, , .

Применяя теорему сложения вероятностей, получим

P (A + B + C) = P (A) + P (B) + P (C) = .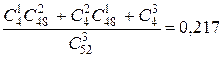

Вероятность события (А + В + С) можно было найти другим способом. Событие D (среди вынутых карт нет тузов) является противоположным событию (А + В + С), поэтому

P (A + B + C) = 1 – P (D),

P (D) = = = 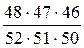0,783,

P (A + B + C) = 1 – 0,783 = 0,217.

Теорема 2. Вероятность суммы двух совместных событий А и В равна сумме вероятностей этих событий без вероятности их совместного появления:

Р (А + В) = Р (А) + Р (В) - Р (А × В).

Пример 3. Чему равна вероятность того, что наудач у взятое двухзначное число окажется кратным либо 2, либо 5?

Решение. Обозначим события:

А – двухзначное число кратно 2,

В – двухзначное число кратно 5.

Нас интересует сумма совместных событий (А + В) – появление числа, кратного либо 2, либо 5, либо обоим вместе.

Количество всех двухзначных чисел n =90, из них благоприятных событию А (число кратно 2) m (A)=45, событию В (число кратно 5) m (B) =18. События А и В имеют общие исходы, так как среди двухзначных чисел есть кратные 2 и 5 одновременно, таких чисел m (AB) = 9.

По теореме сложения вероятностей совместных событий имеем

P (A + B) = P (A) + P (B) – P (AB) = .

Для следующих теорем введем понятие зависимых и независимых событий. Два события А и В называются независимыми, если появление одного из них не влияет на вероятность появления другого (в противном случае события зависимы).

Теорема 3. Вероятность nроизведения двух независимых событий равна nроизведению их вероятностей:

Р (А·В)= Р (А)·Р(В).

Пример 4. Найти вероятность совместного появления «герба» при одновременном бросании двух монет.

Решение. Обозначим события:

А – появление «герба» на первой монете, В – появление «герба» на второй монете. Выпадение «герба» на одной из монет никак не влияет на вероятность его появления на другой, поэтому А и В независимые события,

P (A · B) = P(A) · P (B) = .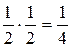

Следствие. Вероятность nроизведения n независимых событий А ₁, А ₂, ..., А_n равна nроизведению их вероятностей:

Р (А ₁· А ₂·... ·А_n) = Р (A ₁)·Р(А ₂)·...· Р (А_n).

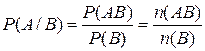Условной вероятностью события А при наличии события В называется вероятность события А, вычисленная при условии, что событие В произошло. Эта вероятность обозначается . Пусть события А и В определены в одном пространстве элементарных событий W, и . Тогда величина называется условной вероятностью события А при условии, что событие В произошло. В формуле через обозначили число элементарных исходов, входящих в событие В, а через - число общих элементарных исходов в событиях А и В.

Пример 5. Опыт состоит в последовательном бросании двух монет. Рассматриваются события:

А - выпадение герба на первой монете;

D - выпадение хотя бы одного герба;

Е - выпадение хотя бы одной цифры;

F - выпадение герба на второй монете.

Определить, зависимы или независимы пары событий:

а) A и E;

б) A и F;

в) D и E.

Решение.

а) А и Е: Р (Е)=3/4; Р (Е/А)=1/2; события зависимы;

б) А и F: Р (А)=1/2; Р (А/F)=1/2; события независимы;

в) D и Е: Р (D)=3/4; Р (D/Е)=2/3; события зависимы.

Теорема 4. Вероятность nроизведениядвух зависимых событий А и В равна nроизведению вероятности настуnления события А на условную вероятность события В nри условии, что событие А уже nроизошло:

Р (А·В)= Р (А)· Р (В / А).

Следствие. Если события А и В независимы, то из теоремы 4 следует теорема 3.

Событие В не зависит от события А, если Р (В / А)= Р (В).

Теорему 4 можно обобщить на n событий.

Теорема 5. Вероятность произведения n зависимых событий А ₁, А ₂ ,..., А_n равна произведению последовательных условных вероятностей:

Р (А ₁ × А ₂×... ×А_n)= Р (А ₁)· Р (А ₂/ А ₁)·...· Р (А_n / А ₁· А ₂·...· А_{n -1}).

Теорема 6. Вероятность наступления хотя бы одного из событий А ₁, А ₂,..., А_n равна разности между единицей и вероятностью произведения отрицаний событий А ₁, А ₂,..., А_n:

Р (А)=1- Р () =

= 1- Р ()· P ()·…· Р ().

Следствие 1. Вероятность наступления хотя бы одного из событий А ₁, А ₂, ..., А_n независимых в совокупности, равна разности между единицей и произведением вероятностей противоположных событий:

Р (А)=1- Р ()· Р ()·...· Р ().

Следствие 2. Если события А ₁, А ₂ ,..., А_n независимы и имеют одинаковую вероятность появиться (Р(А ₁ ) = Р(А ₂ ) = …=Р(А_n) = р, Р(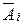) = 1 -р = q), то вероятность появления хотя бы одного из них равна

Р (А)=1- qⁿ.

Пример 6. Студент знает 20 вопросов из 25. Найти вероятность того, что он ответит на три предложенные ему последовательно вопроса?

Решение. Обозначим события:

А – студент ответил на первый вопрос,

В – ответил на второй вопрос,

С – ответил на третий вопрос.

События А, В, С – зависимые, так как вероятность ответов на каждый последующий вопрос зависит от того, ответил или нет студент на предыдущие вопросы. По теореме умножения находим

P (A · B · C)= P (A) · P (A / B) · P (C / AB)= .

Правила (теоремы) сложения и умножения вероятностей редко применяют порознь, обычно они применяются вместе.

Пример 7. Два стрелка произвели по одному выстрелу. Вероятность попадания в мишень первым стрелком равна 0,7, для второго – 0,6. Найти вероятность того, что в мишень попадет хотя бы один стрелок.

Решение. Обозначим события:

А ₁ - попал первый стрелок,

А ₂ - попал второй стрелок.

Событие А (попал хотя бы один стрелок) представляет собой сумму двух совместных событий А = А ₁ + А ₂, вероятность которого равна

Р (А ₁ + А ₂) = Р (А ₁) + Р (А ₂) – Р (А ₁ · А ₂).

События А ₁ и А ₂ независимые, поэтому

Р (А ₁+ А ₂)= Р (А ₁)+ Р (А ₂) – Р (А ₁)× Р (А ₂) = 0,7 + 0,6 – 0,7·0,6=0,88.

Пример 8. Два стрелка сделали по одному выстрелу в мишень, вероятность попадания первого 0,8, а второго - 0,6. Найти вероятность следующих событий:1) событие А - оба попали; 2) событие В - попал один; 3) событие С - попал хотя бы один.

Решение. Обозначим через А ₁, А ₂ события, обозначающие соответственно, что 1-й и 2-й стрелок попали в цель. По условию: Р(А ₁)=0,8; Р(А ₂)=0,6.

Событие A = A ₁· A ₂. Так как события A ₁ и A ₂ независимы

P (A) = P (A ₁· A ₂) = P (A ₁)· P (A ₂) = 0,8·0,6 = 0,48.

B = .

P (B) = 0,2·0,6+0,8·0,4 = 0,12+0,32 = 0,44.

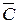- не попал ни один. .

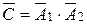P (C) = 1 – P (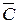) = 1 – 0,2·0,4 = 0,92.

Date: 2016-05-18; view: 673; Нарушение авторских прав