Задачи для самостоятельного решения. 1. При исследовании жирности молока коров все стадо было разбито на три группы

1. При исследовании жирности молока коров все стадо было разбито на три группы. В первой группе оказалось 70%, во второй - 23% и в третьей - 7% всех коров. Вероятность того, что молоко, полученное от отдельной коровы, имеет не менее 4% жирности, для каждой группы коров соответственно равна 0,6, 0,35 и 0,1. Определить вероятность того, что для взятой наудачу коровы жирность молока составит не менее 4%.

Взятая наудачу корова дает молоко жирностью не менее 4%. Найти вероятность того, что эта корова из первой группы.

2. В первой урне 10 деталей, из них 8 стандартных. Во второй 6 деталей, из которых 5 стандартных. Из второй урны переложили в первую одну деталь. Какова вероятность того, что деталь, извлеченная после этого из второй урны, нестандартная?

3. Имеются две урны. В первой – 7 красных шаров и 3 черных, во второй – 3 красных и 4 черных. Из первой урны переложили во вторую один шар, затем, перемешав шары, из второй урны переложили в первую один шар. Найти вероятность того, что шар, извлеченный после этого из первой урны, окажется красным.

4. Перед посевом 90% всех семян было обработано ядохимикатами. Вероятность поражения вредителями растений из обработанных семян равна 0,08, растений из необработанных семян – 0,4. Взятое наудачу растение оказалось пораженным. Какова вероятность того, что оно выращено из обработанного семени?

5. В районе 24 человека обучаются на заочном факультете института, из них шесть – на мехфаке, 12 – на агрофаке и 6 – на экономфаке. Вероятность успешно сдать все экзамены на предстоящей сессии для студентов мехфака равно 0,6, агрофака – 0,76 и экономфака – 0,8. Найти вероятность того, что наудачу взятый студент, сдавший успешно все экзамены, окажется студентом экономфака.

6. В первом ящике из 20 деталей 4 бракованных, во втором - из 30 деталей 5 бракованных. Из первого во второй переложили две детали. Найти вероятность того, что деталь, извлеченная после этого из второго ящика, бракованная.

7. Стрелковое отделение получило 10 винтовок, из которых 8 пристрелянных, две нет. Вероятность попадания в цель из пристрелянной винтовки равна 0,6, а из непристрелянной - 0,4. Какова вероятность, что стрелок из наудачу взятой винтовки попадет в цель при одном выстреле? Стрелок поразил цель. Какова вероятность того, что он стрелял из пристрелянной винтовки?

8. Для посева изготовлены семена 4 сортов пшеницы. Причем, 20% всех семян 1-го сорта, 30% - 2-го сорта, 10% - 3-го сорта и 40 % - 4-го сорта. Вероятность того, что из зерна вырастет колос, содержащий не менее 40 зерен, для 1-го сорта – 0,5,для 2-го – 0,3, для3-го – 0,2, для 4-го – 0,1. Найти вероятность того, что наудачу взятое зерно даст колос, содержащий не менее 40 зерен.

9. Из 25 студентов группы 5 студентов знают все 30 вопросов программы, 10 студентов выучили по 25 вопросов, 7 студентов по 20 вопросов, трое по 10 вопросов. Случайно вызванный студент ответил на два вопроса. Какова вероятность того, что он из тех трех студентов, которые подготовили 10 вопросов.

10. Запасная деталь может находиться в одной из трех партий с вероятностями 0,2; 0,5; 0,3. Вероятности того, что деталь проработает положенное время без ремонта, равны соответственно 0,9; 0,8 и 0,7. Определить вероятность того, что:

а) взятая наудачу деталь проработает положенное время;

б) деталь, проработавшая положенное время, взята из второй или третьей партии.

11. Имеется 5 урн. В первой, второй и третьей находится по 4 белых и 6 черных шаров, в четвертой и пятой урнах по 2 белых и 3 черных шара. Случайно выбирается урна и из нее извлекается шар. Какова вероятность того, что была выбрана четвертая или пятая урна, если извлеченный шар оказался белым?

Схема Бернулли

Пусть некоторый опыт повторяется в неизменных условиях n раз, причём каждый раз может либо наступить (успех), либо не наступить (неудача) некоторое событие А, где Р (А) = р - вероятность успеха, Р (А) = 1- р = q - вероятность неудачи. Тогда вероятность того, что в k случаях из n произойдёт событие А вычисляется по формуле Бернулли

.

Условия, приводящие к формуле Бернулли, называются схемой повторных независимых испытаний или схемой Бернулли. Так как вероятности Р_n (k) для различных значений k представляют собой слагаемые в разложении бинома Ньютона

,

то распределение вероятностей Р_n (k), где 0£ k £ n, называется биномиальным.

При решении задач на использование формулы Бернулли часто применяют следующие формулы.

Вероятность наступления события А:

а) менее k раз

P_n (0)+ P_n (1)+…+ P_n (k- 1);

б) более k раз

P_n (k +1)+ P_n (k +2)+…+P _n (n);

в) не менее k раз

P _n (k)+ P_n (k +1)+…+ P_n (n);

г) не более k раз

P_n (0)+ P_n (1)+…+ P_n (k);

д) хотя бы один раз

1- P_n (0).

Пример 1. Что вероятнее: выиграть у равносильного противника (ничейный исход партии исключен) три партии из четырех или пять из восьми?

Решение. Так как противники равносильны, то вероятность успеха (выиграть партию) равна , вероятность неудачи . По формуле Бернулли находим

,

.

Следовательно, выигрыш трех партий из четырех вероятнее, чем пять партий из восьми.

Пример 2. Всхожесть семян данного сорта оценена вероятностью р=0,8. Каковы вероятности того, что из 5 семян войдет: 0, 1, 2, 3, 4, 5.

Решение. Число опытов равно 5, опыты независимые. Вероятность появления события А (взошло семя) в каждом опыте одинакова и равна р=0,8, вероятность противоположного события q =0,2.

Следовательно, можно воспользоваться формулой Бернулли.

;

;

;

;

;

.

Из примера2 следует, что вероятность P_n (k) для данного n с увеличением m от 0 до 5 сначала возрастает, а затем уменьшается. Число k ₀, при котором P_n (k) имеет наибольшее значение, называется наивероятнейшим числом наступления успеха в n опытах. В приведенном примере k ₀=4. Наивероятнейшее число можно найти из неравенства

.

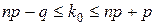Пример 3. Вероятность получения удачного результата при производстве сложного химического опыта равна 2/3. Найти наивероятнейшее число удачных опытов, если общее их число равно 7.

Решение. Вероятность успеха в одном опыте , неудачи , n = 7. Наивероятнейшее число удачных опытов k ₀ найдем из неравенства

;

;

.

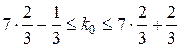Формулой Бернулли удобно пользоваться в том случае, когда число опытов n £10. При большом числе опытов по схеме Бернулли удобнее пользоваться приближенными формулами.

Date: 2016-05-18; view: 1721; Нарушение авторских прав