Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?
Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника
Классическое определение вероятности
|
|
Пусть события
А 1, А 2 ,...,Аn Î S (1.7)
образуют множество элементарных событий. Тогда события из (1.7), которые приводят к наступлению события А, называются благоприятствующими исходами для события А, m (А) - число благоприятствующих исходов. Вероятностью события А называется отношение числа исходов, благоприятствующих наступлению события А, к числу всех возможных исходов
. (1.8)
Из классического определения следуют свойства вероятности:
1) 0< Р (А)<1,
2) Р (W)=1,
3) Р (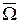
)=0.
А + 
=W - достоверное событие, поэтому Р (А)+ Р ()=1 или
Р ()=1- Р (А).
При вычислении вероятностей по классической схеме приходится решать фактически комбинаторные задачи. При решении конкретной комбинаторной задачи нужно вначале выяснить, каким способом вы будете ее решать: либо непосредственным применением принципов умножения и сложения, либо применением комбинаторных формул, но перед этим нужно выяснить, какой вид комбинации имеется в задаче, важен ли в ней порядок или нет, допускаются повторения или нет.
Пример 1. В урне содержатся 3 синих, 5 красных и 2 белых шара. Из нее наудачу извлекаются сразу два шара. Найти вероятность того, что будут вынуты либо два белых шара, либо два разных цветных шара.
Решение. Поскольку в данной задаче неважен порядок, то для решения будем применять сочетания без повторения (шары не возвращаются обратно в урну). Найдем общее число возможных исходов:
.
Теперь найдем число благоприятствующих возможных исходов. Два белых шара можно вынуть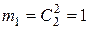 
способом, два разных цветных шара 
способами. Тогда общее число благоприятствующих исходов, в соответствии с принципом сложения, равно 
. Таким образом,
.
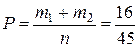Пример 2. Наудачу взятый телефонный номер состоит из 5 цифр. Какова вероятность, что в нем все цифры разные?
Решение. Предположим, что равновозможны появления любой из 10 цифр во всех позициях телефонного номера. Поскольку при составлении пятизначным номеров важен порядок и возможны повторения, то общее число возможных пятизначных номеров будет равно
.
Номера, у которых все цифры разные, – это размещения без повторений
.
Таким образом, искомая вероятность (при сделанном предположении) будет равна
.
Date: 2016-05-18; view: 542; Нарушение авторских прав