Методические указания. Используя программный пакет “Корреляционный анализ много­мерных случайных величин”, удостовериться, что применение алго­рит­мов корреляцион­ного анализа

Используя программный пакет “Корреляционный анализ много­мерных случайных величин”, удостовериться, что применение алго­рит­мов корреляцион­ного анализа позволяет оценить взаимозави­си­мость компонент многомерной случайной величины, выявить харак­тер зависимости (статистический или функциональный), предполо­жить вид статистической или функциональной зависимости (линейный или нелинейный).

Для знакомства с пакетом, перечнем и характером решаемых задач используйте его краткую документацию и встроенную спра­вочную систему.

Следует иметь в виду, что соотношение между коэффициентом корреляции и корреляци­он­ным отношением позволяет сделать следующие выводы:

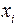а) , если и независимы;

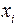б) 1, тогда и только тогда, когда имеется строгая ли­нейная функ­циональная зависимость от ;

в) 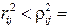1, тогда и только тогда, когда имеется строгая нели­нейная функ­циональная зависимость 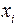от ;

г) 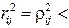1, тогда и только тогда, когда регрессия 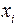по строго линейна, но нет функциональной зависимости;

д) 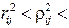1, указывает на то, что не существует функцио­нальной зависи­мости и некоторая нелинейная кривая регрессии "подхо­дит" лучше, чем "наи­лучшая" прямая линия.

То есть, равенство квадрата коэффициента корреляции корреля­ци­онному отношению указывает на то, что для регрессии нельзя найти лучшей кривой, чем прямая линия.

Установить наличие одной из перечисленных ситуаций можно в результате вычисления соответствующих оценок и проверки гипотез.

Date: 2016-05-15; view: 389; Нарушение авторских прав