
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Методические указания. В отличие от задачи принятия решения в условиях риска в данном случае играет роль и состояние среды
|
|
Постановка задачи
В отличие от задачи принятия решения в условиях риска в данном случае играет роль и состояние среды 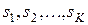 , в котором она находится [].
, в котором она находится [].
Пусть заданы или могут быть определены полезности результатов  при использовании стратегии
при использовании стратегии 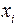 :
: 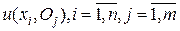 .
.
В зависимости от состояния среды результат  достигается с вероятностью
достигается с вероятностью 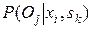 . Наблюдателю неизвестно распределение вероятностей
. Наблюдателю неизвестно распределение вероятностей  . Относительно состояния среды наблюдатель может только высказывать определенные гипотезы. Эти предположения о вероятном состоянии среды являются субъективными вероятностями
. Относительно состояния среды наблюдатель может только высказывать определенные гипотезы. Эти предположения о вероятном состоянии среды являются субъективными вероятностями  . Если бы величины
. Если бы величины  были известны наблюдателю, то мы пришли бы к задаче принятия решения в условиях риска.
были известны наблюдателю, то мы пришли бы к задаче принятия решения в условиях риска.
Критерий Вальда
Это критерий "осторожного наблюдателя". Он оптимизирует полезность в предположении, что среда находится в самом невыгодном для наблюдателя состоянии. По данному критерию решающее правило имеет следующий вид:
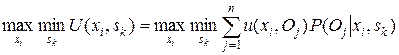 ,
,
По критерию Вальда выбирают стратегию, которая дает гарантированный выигрыш при наихудшем варианте состояния среды.
Критерий Гурвица
Он основан на следующих двух предположениях: среда может находиться в самом невыгодном состоянии с вероятностью 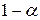 , и в самом выгодном - с вероятностью
, и в самом выгодном - с вероятностью  , где
, где  - коэффициент доверия. Решающее правило имеет вид:
- коэффициент доверия. Решающее правило имеет вид:
 ,
,
где  . Очевидно, что при
. Очевидно, что при 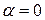 получаем критерий Вальда, а при
получаем критерий Вальда, а при 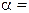
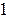 приходим к правилу
приходим к правилу
 ,
,
что представляет собой стратегию "здорового оптимиста".
Критерий Лапласа
Если неизвестны вероятности состояний среды, то в данном случае все состояния среды считаются равновероятными:
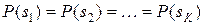 .
.
В результате решающее правило определяется соотношением:
 ,
,
при условии  .
.
Критерий Сэвиджа
Это критерий минимизации сожалений. "Сожаление" – это величина, равная изменению полезности результата при данном состоянии среды относительно наилучшего возможного состояния. Чтобы определить "сожаление", поступаем следующим образом. Строим матрицу  , где
, где
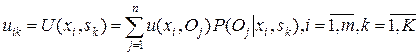 .
.
В каждом столбце этой матрицы находим максимальный элемент
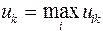 .
.
Его вычитают из всех элементов этого столбца. В результате получаем матрицу сожалений
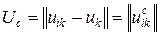 .
.
В качестве оптимальной стратегии выбирают ту 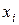 , которая минимизирует "сожаление":
, которая минимизирует "сожаление":
 .
.
Этот критерий минимизирует возможные потери при условии, что состояние среды наихудшим образом отличается от предполагаемого.
В работе предлагается оптимизировать инвестиции денежных средств в ценные бумаги с учетом изменений состояния среды. Интерпретация всех необходимых переменных совпадает с интерпретацией, введенной в лабораторной работе №8. В качестве состояния среды предлагается использовать среднюю температуру воздуха на Земле. Возможны три состояния:  – низкая температура от 0°С до +10°С;
– низкая температура от 0°С до +10°С;  – средняя температура от 10°С до +16,5°С;
– средняя температура от 10°С до +16,5°С;  – высокая температура от 16,5°С до 20°С. Статистика изменения состояния среды в зависимости от месяца года представлена в табл.2.
– высокая температура от 16,5°С до 20°С. Статистика изменения состояния среды в зависимости от месяца года представлена в табл.2.
Таблица 2
Средняя температура воздуха на Земле
| 19,50 | 19,50 | 17,60 | 14,50 | 11,40 | 9,10 | |||||||
| 7,96 | 8,30 | 9,20 | 12,15 | 15,27 | 17,96 | 19,60 | 11,54 | 17,70 | 14,52 | 11,48 | 9,15 | |
| 8,31 | 9,25 | 12,20 | 15,31 | 19,70 | 19,60 | 17,70 | 14,53 | 11,50 | 9,2 | |||
| 8,10 | 8,35 | 9,35 | 12,25 | 15,35 | 18,10 |
Вероятности 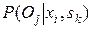 определяются следующим образом. Подсчитывается количество результатов
определяются следующим образом. Подсчитывается количество результатов 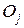 при использовании стратегии
при использовании стратегии 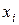 , состояния среды
, состояния среды  и делится на количество всех результатов, произошедших, среда находилась в состоянии
и делится на количество всех результатов, произошедших, среда находилась в состоянии  .
.
Date: 2016-05-15; view: 651; Нарушение авторских прав