Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?
Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника
IV. Теңдеудің екі жақ бөлігін көрсеткіштік функцияға бөлу
|
|
Кейбір көрсеткіштік теңдеулерде екі немесе одан көп көрсеткіштік функциялар берілуі мүмкін. Однай жағдайда көрсетштік функцияның мәні нөлге тең болмайтынын ескеріп теңдеудің екі жақ бөлігін де көрсеткіштік функцияға мүшелеп бөле отырып, оны шешу жолы белгілі теңдеуге келтіреміз.
4- м ы с а л. 3∙16 х + 37 ∙ 36 х ꞊ 81 х теңдеуің шешейік.
Шешуі. Көрсеткіштік функцияның қасиеттерін қолданып, тәңдеудегі
16 х ; 36 х; 81 х өрнектерді түрлендіреміз: 16 х ꞊ 2 4 х; 36 х ꞊ 2 2х ; 81 х ꞊ 3 4х .
Сонда берілген теңдеу 3∙ 2 4х + 37 ∙ 2 2х ∙ 3 2х ꞊ 26 ∙ 3 4х түріне келеді. Енді көрсеткіштік функцияның мәні нөлге тең болмайтынын ескеріа, теңдеудің екі жақ бөлігін 3 4х дәрежесіне мүшелеп бөлейік:
3 ∙ 
+ 37 ∙ 
꞊ 26. = t айнымалысын енгізіп,
3 t2 + 37 t – 26 ꞊ 0квадрат теңдеуін аламыз, оның түрлері
t1 ꞊ 
, t 2꞊ -13. Көрсеткіш функцияның мәндер жиыны тек оң сандар болғандықтан ꞊ көрсеткіштік теңдеуін ғана шешеміз. Бұдан. 2 х ꞊1 немесе х ꞊ 0,5
Жауабы: 0,5.
V. Графигтік тәсілді қолдану. Аталған тәсіл (2) түріндегі көрсеткіштік теңдеуді, яғни ах ꞊ b теңдеуін (3) түріндегі теңдеумен түбірін теңдеумен алмастыруға болмайтын жағдайда қолданылады. Мұндай теңдеудің түбірін анықтау үшін f(x) ꞊ ах және g(x) ꞊ b функцияларының графигін бір координаталық жазықтыққа салып, қиылысу нүктелерін анықтаймыз. Қиылысу нүктелерінің абциссалары берілген көрсеткіштік теңдеудің түбірлері болады
Көрсеткіштік теңдеулер жүйесін шешуді қарастырайық.
Анықтама. Құрамында көрсеткіштік теңдеуі бар теңдеулер жүйесін көрсеткіштік теңдеулер жүйесі деп атаймыз.
Көрсеткіштік теңдеулер жүйесін шешудішешу үшін көрсеткіштік функцияның қаситеттері, көрсеткіштік теңдеулер және теңдеулер жүйесін шешудің тәсілдері қолданылады.
Осыған мысалдар қарастырайық.
5- м ы с а л. 
теңдеулер жүйесін шешейік.
Ш е ш у і. 1) Берілген теңдеулер жүйесін шешу үшін алмастыру тәсілін қолданып, мәндес теңдеулер жүйесін аламыз:
Осыдан 
немесе 
теңдеуі шығады, бұдан
(4 х)2 – 80 ∙ 4 х + 1024 ꞊ 0 аламыз. Енді 4 х ꞊ z деп алып, z2 - 80 z + 1024 ꞊0
квадрат теңдеуін шешеміз. Шыққан квадрат теңдеудің түбірлері
z1 ꞊ 16 және z2 ꞊ 64. Сонда 
және 
х1 ꞊ 2, х2 ꞊ 3, Онда сәйкесінше у 1 ꞊ 3, у 2 ꞊ 2.
Жауабы: (3;2), (2;3).
6- м ы с а л. 
теңдеулер жүйесін шешейік.
Ш е ш у і. Теңдеулер жүйесінде екі көрсеткіштік функция берілген. Алдымен жаңа айнымалылар енгізейік, яғни 
. Сонда екі белгісізі бар сызықтық теңдеулер жүйесін аламыз:
Алгебралық қосу тәсілі бойынша соңғы теңдеулер жүйесінің екінші теңдеуін 2 – ге көбейтеміз: 
Бұдан 5 
꞊ 
немесе 
꞊ 
аламыз. -дың мәнін жүйенің бірінші теңдеуіне қосайық, 
꞊ 
- 
꞊ 2, 
аламыз.
Сонда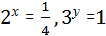 
көрсеткіштік теңдеулері шығады. Оларды шешіп, х ꞊ -2, у ꞊ 0 аламыз.
Жауабы: (-2;0).
Анықтама.
а f(х) > аg(х), a> 0, a ≠1 (1)
түрінде берілген немесе осы түрде келетін көрсеткіштік теңсіздік деп аталады.
Көрсеткіштік теңсіздікті шешу үшін келесі теореманы қолданамыз.
Теорема. Егер a> 1 болса онда, а f(х) > аg(х) теңсіздігі f(x)> g(x) теңсіздігімен; егер 0 < a < 1 болса, онда а f(х) > аg(х) теңсіздігі f(x) < g(x)
теңсіздігімен мәндес болады.
Д ә л е л д е у. Дәлелдеу үшін (1) теңсіздіктің екі жағын аg(х) өрнегіне бөліп,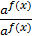 
> 1 теңсіздігін аламыз.
Соңғы теңсіздікті а f(х) - g(х) > 1 теңсіздігіне келтіреміз. Енді f(х) - g(х ) = t белгілеуін енгізсек, 
> 1 теңсіздігі шығады. Осы теңсіздікті шшу үшін a> 1 және 0 < a < 1 екі жағдайын қарастырсақ жеткілікті.
Егер a> 1 болса, онда > 1 теңсіздігі орындалу үшін t > 0 болуы қажет,яғни f(х) - g(х ) > 0. Бұдан f(х) > g(х ) теңсіздігін аламыз.
Date: 2016-06-09; view: 1515; Нарушение авторских прав