Решение. а) рассчитаем трехзвенные скользящие суммы и трехзвенные скользящие средние уровни (графы 3 и 4)

а) рассчитаем трехзвенные скользящие суммы и трехзвенные скользящие средние уровни (графы 3 и 4)

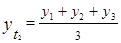= = = 13,30;

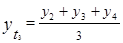= = = 13,37;

= = = 14,63 и т. д.

б) вычислим средний годовой абсолютный прирост валового сбора сахарной свеклы за весь рассматриваемый период времени:

= = 0,9375 (млн. т).

Рассчитаем механически выравненные уровни ряда динамики () следующим образом (графа 5):

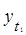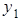= ; ; и т. д.

Полученные числовые значения представим в таблице:

Год		Скользящие суммы	Скользящие средние	Механически выравненный ряд
	13,9	–	–	13,9000
	10,8	39,9	13,30	14,8375
	15,2	40,1	13,37	15,7750
	14,1	43,9	14,63	16,7125
	14,6	44,4	14,8	17,6500
	15,7	49,7	16,57	18,5875
	19,4	56,9	18,97	19,5250
	21,8	62,7	20,87	20,4625
	21,4	–	–	21,4000

Если скользящие средние величины рассчитывают из четного числа уровней, то производят их центрирование.

в) линейная функция, отражающая изменение уровней ряда динамики имеет следующий вид: ,

где 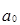и – параметры линейной функции;

– параметры времени.

Все необходимые расчеты представим в следующей таблице, в столбце 3 которой введем параметры времени .

Год
	13,9		13,9		11,4556
	10,8		21,6		12,6722
	15,2		45,6		13,8889
	14,1		56,4		15,1056
	14,6		73,0		16,3222
	15,7		94,2		17,5389
	19,4		135,8		18,7556
	21,8		174,4		19,9722
	21,4		192,6		21,1889
Итого	146,9		807,5		146,9

Для нахождения параметров линейной функци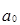и и составляют следующую систему уравнений:

Вычисленные в таблице величины подставим в систему уравнений

Решая систему, получаем, что = 1,21667и 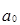= 10,23889, т. е.уравнение линейной функции имеет вид

.

На основе уравнения линейной функции для каждого года рассчитаем теоретические значения уровней ряда (столбец 6).

Изобразим полученные данные графически (рис. 6).

Рис. 6. Выявление основной тенденции изменения уровней рядов динамики

Используя полученное уравнение функции, можно рассчитать перспективное значение ряда динамики. Например, определим валовой сбор сахарной свеклы в 2010 г. Для 2010 г. t = 14

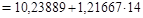= 27,27 млн. т.

Если параметры времени задаются таким образом, что их сумма равна 0 ( 0), то параметры линейной функции и вычисляют по формулам

и .

Для параболы второго порядка, которая выражается уравнением 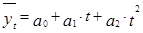, система уравнений для расчета параметров функции принимает вид

При анализе рядов динамики прибегают к интерполяции и экстраполяции.

Метод интерполяции заключается в определении неизвестных уровней внутри существующего ряда динамики.

Метод экстраполяции состоит в расчете уровней за пределами существующего ряда динамики на основе выявленных закономерностей при изучении изменения явления, т. е. строится прогноз на перспективу ( ).

Для этого используются следующие формулы:

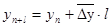и ,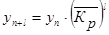

где – экстраполируемый уровень;

– конечный уровень ряда динамики;

– срок прогноза;

– среднегодовой абсолютный прирост за рассматриваемый период;

– среднегодовой коэффициент роста за рассматриваемый период.

Date: 2016-01-20; view: 469; Нарушение авторских прав