
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Тема 6. Выборочное наблюдение
|
|
Выборочным называется несплошное наблюдение, при котором обследованию и изучению подвергается не вся исходная совокупность, а специально отобранная ее часть.
Средняя (стандартная) ошибка выборки ( ) характеризует среднюю величину возможных расхождений средней выборочной величины (
) характеризует среднюю величину возможных расхождений средней выборочной величины ( ) и генеральной средней (
) и генеральной средней (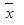 ), т. е. справедливо соотношение
), т. е. справедливо соотношение  .
.
Предельная ошибка выборки (  ) рассчитывается по формуле
) рассчитывается по формуле
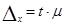 ,
,
где t – коэффициент доверия, зависящий от вероятности, с которой можно гарантировать, что предельная ошибка не превысит t -кратную среднюю ошибку, т. е. всегда будет выполняться неравенство
 .
.
Значения коэффициента доверия при соответствующей вероятности:
| Вероятность, % | 68,3 | 95,0 | 95,4 | 99,0 | 99,7 | 99,9 |
| Коэффициент доверия, t | 1,00 | 1,96 | 2,00 | 2,58 | 3,00 | 3,28 |
Виды методов отбора единиц в выборочную совокупность: повторный и бесповторный.
Виды способов организации отбора единиц в выборочную совокупность: собственно-случайный; механический; типический; серийный.
Формулы для расчета средней ошибки выборки:
| Вид отбора | Метод отбора | Средняя ошибка выборки | |
| для средней | для доли | ||
| Собственно-случайный | повторный | 
| 
|
| бесповторный | 
| 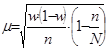
|
О к о н ч а н и е
| Механический | повторный | 
| 
|
| бесповторный | 
| 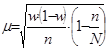
| |
| Типический | повторный | 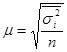
| 
|
| бесповторный | 
| 
| |
| Серийный | повторный | 
| 
|
| бесповторный |  
| 
|
где  – дисперсия выборочной совокупности;
– дисперсия выборочной совокупности;
N – число единиц генеральной совокупности;
n – число единиц выборочной совокупности;
w – доля единиц совокупности, обладающих данным альтернативным признаком в выборочной совокупности;
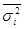 – средняя из внутригрупповых дисперсий;
– средняя из внутригрупповых дисперсий;
r – число отобранных серий;
R – число серий в генеральной совокупности;
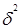 – межгрупповая дисперсия;
– межгрупповая дисперсия;
 – средняя из внутригрупповых дисперсий для доли;
– средняя из внутригрупповых дисперсий для доли;
 – межсерийная дисперсия для доли.
– межсерийная дисперсия для доли.
Пример 1. В городе проживает 250 тыс. семей. Для определения среднего числа детей в семьях города была организована 2%-ная случайная бесповторная выборка семей. Получено распределение семей:
| Число детей в семье, чел. | Количество семей, единиц |
| 2 500 | |
| 1 200 | |
| Итого | 5 000 |
С вероятностью 99,9% определить пределы, в которых находится среднее число детей в семьях города.
Решение. Все предварительные расчеты представим в таблице:
Число детей, 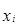
| Количество семей, 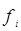
| 
| 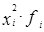
|
| 2 500 | 2 500 | 2 500 | |
| 1 200 | 2 400 | 4 800 | |
| 1 200 | 3 600 | ||
| 1 600 | |||
| Итого | 5 000 | 6 500 | 12 500 |
Рассчитаем среднюю величину и дисперсию выборочной совокупности

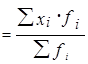 = 1,3 чел.
= 1,3 чел.
 = 2,5.
= 2,5.
 = = 2,5 – (1,3)2 = 0,81.
= = 2,5 – (1,3)2 = 0,81.
Вычислим предельную ошибку выборки
 =
=  =
= 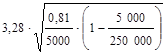 = 0,0126 (чел.).
= 0,0126 (чел.).
Находим пределы генеральной средней величины
1,3 – 0,0126  1,3 + 0,0126,
1,3 + 0,0126,
т. е. с вероятностью 99,9% можно утверждать, что в среднем на каждые три семьи в городе приходится 4 ребенка.
Пример 2. Проводился 10% бесповторный типический отбор работников предприятия с целью оценки потерь из-за временной нетрудоспособности. Получены следующие результаты обследования:
| № отдела | Численность работников, чел. | Обследовано, чел. | Число дней временной нетрудоспособности за год | |
| средняя | дисперсия | |||
| 2 000 | ||||
| 3 000 | ||||
| 1 000 |
С вероятностью 95,4 определить предельную ошибку выборки.
Решение. Вычислим среднюю величину в выборочной совокупности


 = 14,5 дней.
= 14,5 дней.
Определим среднюю из внутригрупповых дисперсий
 = 31,5.
= 31,5.
Предельная ошибка выборки рассчитывается следующим образом:
 = 0,435 (дней),
= 0,435 (дней),
т. е. с вероятностью 95,4% можно сделать вывод о том, что среднее число дней временной нетрудоспособности одного работника в целом по предприятию находится в пределах от 14,065 до 14,935 дней.
Необходимая численность единиц выборочной совокупности определяется из соответствующих соотношений, используемых при расчете предельных ошибок выборки.
| Виды выборки | Повторный отбор | Бесповторный отбор |
| Собственно случайная Механическая | n = 
| n = 
|
| Типическая | n = 
| n = 
|
| Серийная | n = 
| n = 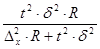
|
Пример 3. В 100 туристических агентствах города предполагается провести обследование среднемесячного количества реализованных путевок методом механического бесповторного отбора.
Каков должен быть объем выборки, чтобы с вероятностью 68,3% предельная ошибка не превышала 3 путевок, если по данным пробного обследования дисперсия составляет 225?
Решение. Определим необходимую численность выборки
 агентств.
агентств.
Для проведения обследования должно быть отобрано не менее 20 агентств.
Date: 2016-01-20; view: 563; Нарушение авторских прав