Основные теоремы о дифференциалах

1)Дифференциал суммы, произведения и частного двух дифференцируемых функций определяются следующими формулами: , ,

2)Дифференциал сложной функции равен произведению производной этой функции по промежуточному аргументу на дифференциал этого промежуточного аргумента.

32:Таблица дифференциалов.

1.

2.

3.

4.

5.

6. ;

7.

8.

9.

10.

11.

12.

13.

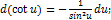
14.

15.

16.

17.

33:Применение дифференциала к приближенным вычислениям.

Как уже известно, приращение функции в точке X можно представить в виде , где при , или 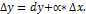Отбрасывая бесконечно малую более высокого порядка, чем , получаем приближенное равенство , причем это равенство тем точнее, чем меньше

Это равенство позволяет с большой точностью вычислить приближенно приращение любой дифференцируемой функции. Дифференциал обычно находится значительно проще, чем приращение функции, поэтому формула широко применяется в вычислительной практике.

34:Дифференциалы высших порядков.

Пусть дифференцируемая функция, а ее аргумент x – независимая переменная. Тогда ее первый дифференциал есть также функция x; можно найти дифференциал этой функции.

Дифференциал от дифференциала функции называется ее вторым дифференциалом (или дифференциалом второго порядка) и обозначается или

35:Некоторые теоремы о дифференцируемых функциях.

Рассмотрим ряд теорем, имеющих большое теоретическое и прикладное значение.

Теорема Ролля: Если функция непрерывна на отрезке , дифференцируема на интервале и на концах отрезка принимает одинаковые значения , то найдется хотя бы одна точка , в которой производная 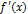обращается в нуль, то есть .

Теорема Коши: Если функция и непрерывны на отрезке , дифференцируемы на интервале , причем для , то найдется хотя бы одна точка такая, что выполняется равенство .

Теорема Лагранжа: Если функция непрерывна на отрезке , дифференцируема на интервале , то найдется хотя бы одна точка такая, что выполняется равенство .

36: Правила Лопиталя.

Теорема (Правило Лопиталя раскрытия неопределенностей вида ). Пусть функции и непрерывны и дифференцируемы в окрестности точки и обращаются в нуль в этой точке: . Пусть в окрестности точки . Если существует предел , то

Теорема (Правило Лопиталя раскрытия неопределенностей вида ). Пусть функция непрерывны и дифференцируемы в окрестности точки , в этой окрестности = , Если существует предел то .

Правило Лопиталя применяется для раскрытия неопределенностей вида и , которые называют основными.

Date: 2016-01-20; view: 1559; Нарушение авторских прав