Обратная функция

Пусть задана функция у =f(x) с областью определения D и множеством значений E. Если каждому значению y соответствует единственное значение x , то определена функция x с областью определения E и множеством значений D. Такая функция называется обратной к функции f(x) и записывается в следующем виде x =f в степени -1(у). Про функции у =f(x) и ) говорят, что они являются взаимно обратными. Чтобы найти функцию ), обратную к функции у =f(x) достаточно решить уравнение f(x)= у относительно х, (если это возможно.) Из определения обратной функции вытекает, что функция у =f(x) имеет обратную тогда и только тогда, когда функция f(x) задает взаимно однозначное соответствие между множествами Dи E. Отсюда следует, что любая строго монотонная функция имеет обратную. При этом если функция возрастает(убывает), то обратная функция также возрастает(убывает).Заметим, что функция у =f(x) и обратная ей изображаются на одной и той же кривой, т. е. графики их совпадают. Сложная функция.Пусть функция у =f(u) определена на множестве D, а функция на множестве D1, причем для 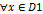соответствующее значение . Тогда на множестве D1 определена функция , которая называется сложной функцией от x(или суперпозиций заданных функций, или функции от функции).Переменную называют промежуточным аргументом сложной функции.