Статистическая проверка результатов

Важным этапом обработки результатов многофакторного эксперимента является статистическая обработка, обязательная, естественно, для любых экспериментальных методов. Смысл статистической проверки состоит в том, чтобы сопоставить результаты обработки экспериментальных данных с возможной -погрешностью их определения и на основании этого, во-первых, выделить достаточно достоверную (на фоне случайных ошибок) информацию, а, во-вторых, проверить достаточно ли полно в полученной статистической модели (уравнении регрессии) использована информация, содержащаяся в результатах эксперимента. Первая операция называется проверкой значимости коэффициентов уравнения регрессии, а вторая - проверкой адекватности модели.

Начальной операцией в статистическом анализе является определение дисперсии воспроизводимости (или дисперсии отклика 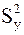) - величины, количественно характеризующей случайные погрешности эксперимента. Она может определяться по разбросу результатов измерения отклика у_ui в одной и той же точке плана.

Дисперсия, характеризующая степень рассеяния результатов параллельных (повторных) опытов (т.е. опытов при одном и том же сочетании уровней факторов - одной точки плана) около среднего значения, вычисляется по формуле

и тогда

(3.11)

где i=1, 2,..., m - число повторных опытов при u-м сочетании уровней факторов; у_ui - результат отдельного опыта; - среднее арифметическое повторных опытов; m-1=f_u - число степеней свободы выборки у_u1, у _u2,..., у _um, равное числу опытов минус единица, ибо одна степень свободы использована для вычисления среднего (числом степеней свободы в планировании эксперимента называется разность между числом опытов и числом коэффициентов (или констант), которые уже вычислены по результатам этих опытов независимо друг от друга).

Если повторные опыты проводятся в каждой точке плана, т.е. в каждой строке матрицы имеется несколько результатов измерений у_ui при тех же значениях х., то дисперсия всего плана эксперимента получается в результате усреднения дисперсий в каждой строке (точке) плана:

(3.12)

Этой формулой можно пользоваться, если число повторных опытов одинаково в каждой строке матрицы. Число степеней свободы дисперсии воспроизводимости f_y=N(m-1).

Естественно, что суммируемые дисперсии должны быть однородны, т.е. среди них нет такой, которая бы значительно превышала все остальные. Проверка однородности дисперсий проводится с помощью F-критерия (статистического критерия Фишера).

Две дисперсии значимо отличаются друг от друга (неоднородны -их нельзя суммировать), если

где F_эксп - экспериментальное значение F-критерия, равное отношению большей дисперсии к меньшей; - табличная величина F-критерия при 5 %-ном уровне значимости (обычном в технических задачах); f_us=f₁, - число степеней свободы для числителя, равное числу степеней свободы большей дисперсии; =f₂ - число степеней свободы для знаменателя, равное числу степеней свободы меньшей дисперсии.

На практике чаще всего каждая вектор-строка плана эксперимента реализуется лишь один раз, а дисперсия воспроизводимости определяется по нескольким повторным опытам в центре плана, т.е. 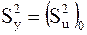. В двигателестроении, где опыты недешевы и организационно-методически трудоемки, такой подход используется практически всегда.

Проверка значимости коэффициентов - исключение из полученного уравнения регрессии коэффициентов (и, естественно, соответствующих членов), по абсолютному значению меньших доверительного интервала их вычисления (т.е. лежащих в пределах возможной случайной погрешности), проводится следующим образом. Определяется сначала дисперсия коэффициента регрессии , так как коэффициент находится по N измерениям. Доверительный интервал коэффициента

где - табличное значение t-критерия при 5 %-ном уровне значимости со степенью свободы f_y, с которой определялось значение 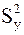; - стандарт коэффициента b_j. Коэффициент b_j считается незначимым, т.е. его следует не учитывать, если

(3.14)

При проверке адекватности модели выясняется, насколько хорошо уравнение регрессии описывает экспериментальные данные. Дисперсия адекватности характеризует среднее квадратическое отличие экспериментальных значений отклика от соответствующих значений, вычисленных по уравнению регрессии.

Дисперсия адекватности рассчитывается разными способами в зависимости от реализации матрицы планирования. Если опыты в матрице планирования не дублируются, а дисперсия воспроизводимости определяется на основании повторных опытов в нулевой точке или из предварительных экспериментов, то дисперсия адекватности рассчитывается по формуле

(3.15)

где у_u - значение целевой функции в u-й строке матрицы; -расчетное по уравнению регрессии значение отклика в той же строке матрицы; f_ад=N-(k+l) - число степеней свободы для дисперсии адекватности, равное числу различных опытов, результаты которых используются для расчета коэффициентов регрессии, минус число определяемых коэффициентов; N - число опытов (строк) в матрице планирования; k - число значимых факторов (коэффициентов); l -число значимых коэффициентов для взаимодействий второго и более высоких порядков.

Если m=const и m>1, то

(3.16)

Модель (полученное уравнение регрессии) адекватна, т.е. хорошо согласуется с изучаемым процессом, объектом, если выполняется неравенство

(3.7)

где 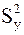- дисперсия воспроизводимости с числом степеней свободы f_y=N(m-1) (для m=1 f=N); - табличное значение критерия Фишера при 5 %-ном уровне значимости.

Задача интерполяции решена, если получено адекватное уравнение регрессии. При неадекватном уравнении можно воспользоваться рекомендациями разд. 3.5, чтобы сделать все-таки уравнение регрессии адекватным. Если это не удается, то можно взять для описания полином большей степени, а N неизвестных коэффициентов регрессии определить, используя метод наименьших квадратов.

Date: 2016-01-20; view: 684; Нарушение авторских прав