
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Определение коэффициентов полинома первой степени
|
|
Осуществив все запланированные опыты, необходимо далее обработать эксперимент, т.е. вычислить значения коэффициентов уравнения регрессии, основываясь на измеренных значениях откликов у1, у2, у3 и у4 (табл. 3.2):
 (3.6)
(3.6)
Нетрудно убедиться (например, решая систему четырех уравнений типа (3.6) с подставленными в левую и правую части значениями отклика и факторов из табл. 3.2), что коэффициенты уравнения регрессии (или просто коэффициенты регрессии) определяются выражениями

 (3.7)
(3.7)

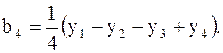
Дисперсия  , с которой определяются коэффициенты регрессии в многофакторном плане (табл. 3.2).
, с которой определяются коэффициенты регрессии в многофакторном плане (табл. 3.2).


Таким образом, средняя квадратическая погрешность по многофакторному плану в  раз меньше, чем по однофакторному плану экспериментов (см. табл. 3.1), т.е. при равном числе опытов и на прежнем оборудовании многофакторный план позволяет получить более точные результаты.
раз меньше, чем по однофакторному плану экспериментов (см. табл. 3.1), т.е. при равном числе опытов и на прежнем оборудовании многофакторный план позволяет получить более точные результаты.
Для удобства вычисления коэффициентов план (см. табл. 3.2) дополняют еще двумя столбцами и представляют в виде матрицы планирования эксперимента (табл. 3.4).
В табл. 3.4 x0 называется фиктивной переменной, всегда равной +1, а столбец x1x2 получается почленным перемножением элементов xiu столбцов x1 и x2.
Сравнив чередование знаков в числителях выражений (3.7) и соответствующих вектор-столбцов факторов (включая x0 и x1x2), видим их идентичность. Поэтому можно предложить общую формулу для определения значений коэффициентов регрессии:

i=0, 1, 2, …, k; u= 1, 2, …, N. (3.8)
Таблица 3.4
| N | x0 | x1 | x2 | x1x2 | yu |
| +1 | -1 | -1 | +1 | y1 | |
| +1 | +1 | -1 | -1 | y2 | |
| +1 | -1 | +1 | -1 | y3 | |
| +1 | +1 | +1 | +1 | y4 |

Информация для проведения опытов

Информация для расчета коэффициентов
Таким образом, для определения каждого из коэффициентов регрессии следует алгебраически просуммировать результаты всех опытов yu, взяв их со знаками соответствующего вектор-столбца, и разделить сумму на число опытов. Для вычисления коэффициента b12 в формуле (3.8) фактором следует считать произведение x1x2 Введение фиктивной переменной х0 делает эту формулу пригодной и для коэффициента b0.
Поясним подробней, в чем смысл взаимодействия x1x2. Обратим внимание прежде всего на то, что, несмотря на наличие в (3.6) члена со взаимодействием x1x2, зависимость отклика от каждого фактора остается линейной, как и в (3.4). Однако если в (3.4) влияние фактора x1 на у выражалось значением коэффициента b1 при любом значении x2, то согласно (3.6) при x2=0 у=b0+b1x1, в то время как при x2=+1 у=b0+(b1+b12)x1, а при x2=-1 у=b0+(b1-b12)x1. Другими словами, влияние каждого из факторов на отклик у различно в зависимости от того, чему равен второй фактор. Поэтому наклон поверхности отклика различен в различных частях области эксперимента. Поверхность отклика (3.6) - гиперболический параболоид, в то время как (3.4) - плоскость. В этом и заключается физический и геометрический смысл взаимодействия факторов.
Таблица 3.5
| N | zi | yu | |||||||
| x0 | x1 | x2 | x3 | x1x2 | x1x3 | x2x3 | x1x2 x3 | ||
| + | - | - | - | + | + | + | - | y1 | |
| + | + | - | - | - | - | + | + | y2 | |
| + | - | + | - | - | + | - | + | y3 | |
| + | + | + | - | + | - | - | - | y4 | |
| + | - | - | + | + | - | - | + | y5 | |
| + | + | - | + | - | + | - | - | y6 | |
| + | - | + | + | - | - | + | - | y7 | |
| + | + | + | + | + | + | + | + | y8 |

Информация для проведения опытов

Информация для расчета коэффициентов
Обратимся к ПФЭ 23. На основе плана эксперимента (табл. 3.3) построена матрица планирования (табл. 3.5).
Часто при составлении матрицы планирования вместо +1 и -1 условно записывают лишь "+" или "-", понимая под этим верхний и нижний уровни кодированных факторов. Так сделано в табл. 3.5.
Первый столбец матрицы - фиктивная переменная. Столбцы взаимодействий получаются перемножением столбцов плана эксперимента сначала попарно, а затем и всех трех. Реализация такого плана эксперимента позволяет получить уравнение регрессии:
 (3.9)
(3.9)
Это уравнение содержит свободный член, линейные члены, три парных взаимодействия и тройное взаимодействие. Восемь неизвестных коэффициентов полинома могут быть определены по результатам восьми опытов, каждый из которых, как уже указывалось, дает одно линейное уравнение, связывающее между собой коэффициенты bi.
Как и для ПФЭ 22, в случае ПФЭ 23 свойства плана таковы, что результаты решения составленной системы из восьми линейных уравнений выражаются простой формулой
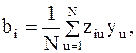 (3.10)
(3.10)
где под ziu понимается либо фактор, либо взаимодействие.
Изложенное выше для ПФЭ 22 и ПФЭ 23 легко распространяется на эксперимент для k>3. Число опытов для k=4, 5, 6,... будет соответственно 16, 32, 64,... Столько же членов будет в правой части уравнения регрессии, включающего все парные, тройные и прочие взаимодействия, в том числе - одно высшее взаимодействие -произведение всех факторов. Коэффициенты уравнения определяются выражением (3.10).
В предыдущем подразделе при рассмотрении свойств ПФЭ отмечалась его ортогональность, т.е. равенство нулю суммы построчных произведений любых столбцов. Матрица планирования также ортогональна. Это придает полученному уравнению регрессии важное для практики свойство, заключающееся в том, что все коэффициенты bi найдены независимо.
Обратим внимание на выражения (3.7). Каждый коэффициент выражается только через результаты опытов уu, и расчет коэффициентов можно вести в любом порядке, так как значения ранее найденных коэффициентов не входят в правую часть выражения для вычисления следующего коэффициента.
Представим себе, что по каким-либо причинам один из коэффициентов уравнения (3.6) не такой, как следует из выражений (3.7) и (3.8), а, например, округлили его значение, допустили ошибку в вычислениях или вообще решили исключить соответствующий член уравнения регрессии. При этом все остальные коэффициенты сохранят неизменную величину.
Это утверждение не очевидно, как может показаться на первый взгляд. Действительно, каждый, кто хоть раз занимался построением уравнения регрессии или, проще говоря, аппроксимировал аналитической зависимостью набор экспериментальных точек, знает, что при попытке как-либо скорректировать вид выбранного уравнения или какой-либо из коэффициентов приходится заново определять значения всех остальных коэффициентов уравнения. При этом бывает, что изменяются не только значения, но даже и знаки отдельных коэффициентов правой части уравнения. В результате скорректированное уравнение может по-прежнему удовлетворительно описывать результаты опытов, однако оценка вклада каждого фактора в итоговый результат окажется иной. Между тем для инженера, анализирующего данные проведенного эксперимента, чрезвычайно важна неискаженная информация именно о роли каждого из факторов, ибо на этом будут основываться иногда очень серьезные практические выводы.
Случайный же набор экспериментальных точек требованию ортогональности в общем случае не удовлетворяет, и именно поэтому коэффициенты уравнения, полученные традиционным, однофакторным способом, оказываются увязанными между собой. В этом случае считают, что имеет место смешивание эффектов, которое заставляет с осторожностью относиться к анализу полученных данных.
Независимость коэффициентов уравнения регрессии, полученного по результатам многофакторного ПФЭ. значительно увеличивает информативность полученных данных, так как придает каждому коэффициенту регрессии физический смысл коэффициента влияния соответствующего фактора.
Из формул (3.7) и (3.8) видно, что каждый коэффициент уравнения регрессии в многофакторном плане экспериментов вычисляется по результатам всех проведенных опытов, в то время как в однофакторном традиционном плане первого порядка каждый коэффициент bi определялся бы лишь по двум опытам. Это, как убедились выше, способствует повышению точности определения коэффициентов - снижает случайную погрешность результата при той же погрешности первичных измерений.
Кроме этого видно, что, несмотря на равное число опытов в обоих планах, в многофакторном плане можно получить четыре члена уравнения (3.6), а в однофакторном - только три члена уравнения (3.4). Коэффициент b12 взаимодействия факторов определить не удается. Таким образом, и информативность многофакторного плана выше.
Наконец, еще одно соображение следует учитывать при сравнительной оценке традиционного однофакторного и многофакторного планов для сложного технического объекта. Пусть в серии традиционных, однофакторных опытов, проводимых для изучения влияния фактора x1 при фиксированных значениях остальных факторов, хотя бы один из них, например x2, не удалось удержать на выбранном уровне. Причем это выяснилось только при обработке результатов эксперимента. Если не удается привести отклик к назначенному постоянному уровню x2 (а для этого необходимы дополнительные сведения о характеристиках объекта), то такие точки использовать не удается - их нельзя нанести на график у=f(x1). В многофакторном же плане, в котором одновременно изменяются значения всех факторов, а результат -характеристика в виде уравнения регрессии - определяется обработкой всех измерений отклика, отклонения какого-либо фактора от плана эксперимента особенно не опасны. Правда, план и соответственно уравнение регрессии утеряют некоторые оптимальные свойства, однако при небольших отступлениях от намеченного оптимального плана это не будет иметь практического значения.
Date: 2016-01-20; view: 1168; Нарушение авторских прав