Многофакторный эксперимент

Математическая статистика и теория вероятностей предлагают способы построения такого оптимального плана проведения опытов, который обеспечивает получение требуемых данных с заданной точностью при минимальном объеме испытаний.

В практике двигателестроения исследуются сложные технические системы, функционирование которых определяется несколькими факторами: x₁, x₂, x₃,..., x_n. Инженер-исследователь сначала проводит серию опытов, в которых задается ряд значений одной из независимых переменных, например x₁-(x₁⁽¹⁾, x₁⁽²⁾, x₁⁽³⁾,...) при неизменных значениях всех остальных факторов x₂, x₃,..., x_k. В результате определяется у=f(x₁). Затем в следующей серии опытов изменяют значения второго фактора x₂ при фиксированных, постоянных значениях x₁, x₂, x₄,..., x_k и определяют зависимость у=j(x₂). Поочередно проделывают это для остальных факторов x₃, x₄,..., x_k и в итоге получают представление о зависимости у=у(x₁, x₂,..., x_k). Такой эксперимент называется однофакторным и на первый взгляд представляется единственно правильным, позволяющим в явном виде выявить влияние каждого фактора x₁,..., x_k на изучаемые отклики у, у₁, у₂, … объекта исследования.

Между тем в теории эксперимента убедительно показано, что при исследовании сложных технических систем следует не поочередно, а одновременно изменять значения всех факторов x₁,.., x_k от опыта к опыту в каждом из них. Такой эксперимент называется многофакторным и является альтернативой традиционной серии однофакторных экспериментов.

Неизбежно возникает вопрос, не будут ли перепутаны эффекты, вызываемые различными факторами, если в каждом из проводимых опытов изменять значения сразу нескольких факторов x₁,..., x_k. Действительно, изменение отклика у от опыта к опыту при многофакторном эксперименте происходит под влиянием одновременного изменения ряда факторов. Однако если план эксперимента (т.е. сочетания значений факторов, а также число и порядок реализации опытов) выбран с соблюдением специальных правил, то одновременное варьирование нескольких факторов не приводит к неопределенности в оценке отклика у. После несложной математической обработки можно определить влияние каждого из факторов x₁,..., x_k в отдельности на целевую функцию у с точностью, более высокой, чем в равной по объему серии традиционных однофакторных опытов.

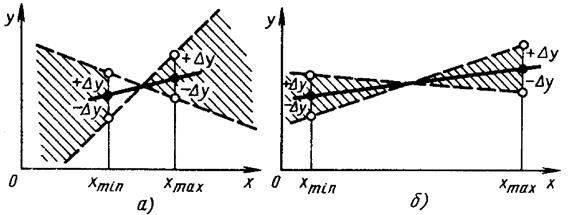
Рис. 3.2. Погрешность линейной интерполяции при разных интервалах x_min…x_max:

·, о - истинные и измеренные значения у; ± Dу — погрешность измерения

Для увеличения достоверности результатов опытов целесообразно расширять область эксперимента - оптимально использовать пространство независимых переменных (факторов). Более наглядно это поясняется графически. На рис. 3.2, a видно, что если два значения x_min и x_max, в которых проводятся измерения, располагаются близко друг к другу, то даже небольшая погрешность в эксперименте ± Dу приводит к большому рассеянию возможных интерполяционных зависимостей (для линейной зависимости у=f(x) зона рассеяния заштрихована). Такие точки x_min и x_max можно назвать «плохими» экспериментальными точками. На рис. 3.2, б видно, что зона рассеяния линейной интерполяции при неизменном значении ±Dу меньше благодаря увеличению интервала x_min…x_max. Эти точки, по-видимому, можно назвать «хорошими». Следует, однако, помнить, что в реальных исследованиях невозможно увеличивать размеры исследуемого пространства по крайней мере по двум причинам. Во-первых, технология эксперимента может этого не позволить, а во-вторых, линейной аппроксимации может быть недостаточно и тогда необходимы еще опыты для получения у=f(x) более высоких степеней.

С ростом числа факторов (независимых переменных) эффективность многофакторного плана существенно увеличивается. Этот факт легко доказывается в многомерной математической статистике, констатирующей, что с увеличением числа k факторов x_k, одновременно участвующих в опыте, радиус обследуемой сферы многомерного пространства увеличивается (а следовательно, увеличивается, как мы убедились выше, точность эксперимента) в раз просто из-за свойств многомерного пространства, не требуя увеличения интервалов x_min…x_max по каждой независимой переменной в отдельности. В теории планирования эксперимента в этом случае считают, что факторное пространство используется оптимально, т.е. учитывают все существенно влияющие на отклик факторы.

Ниже будут даны правила, позволяющие применительно к различным задачам построить оптимальный план многофакторного эксперимента, полностью реализующей указанные преимущества.

В заключение необходимо отметить, что если в химической промышленности, металлургии, агротехнике методы многофакторного эксперимента являются общепринятыми, то в авиационной технике большинство испытаний сложных авиационных объектов пока проводится прочно устоявшимися методами однофакторного эксперимента. Это обусловливается множеством как объективных, так и субъективных причин.

Очень трудно, например, конструктору-двигателисту решиться на многофакторный подход при проверке доводочных мероприятий. Нелегко поверить, не будучи хорошо знакомым с теорией планирования эксперимента, в то, что из «смешанного» эксперимента удается выяснить эффективность каждого из нескольких реализованных конструкторских мероприятий. Риск получения неправильного результата в назначенный, всегда сжатый срок часто заслоняет все другие соображения, в том числе и стоимость эксперимента. Заказчик авиационной техники, действуя по установленным положениям, обычно хочет видеть конкретные характеристики объекта и непосредственно измеренные на необходимых режимах экспериментальные значения - тягу, удельный расход топлива, КПД и др. Пересчет по экспериментально полученному уравнению у=f(x_k) для заказчика пока неубедителен, даже если имеются неопровержимые доказательства, что многофакторный эксперимент дает более высокую точность результата.

Date: 2016-01-20; view: 2030; Нарушение авторских прав