
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Понятие о моделях
|
|
Во многих задачах требуется установить и оценить зависимость изучаемой случайной величины Y от одной или нескольких других величин. Две случайные величины могут быть связаны либо функциональной зависимостью, либо зависимостью другого рода, называемой статистической, либо быть независимыми.
Строгая функциональная зависимость реализуется редко, так как обе величины или одна из них подвержены еще и действию случайных факторов, причем среди них могут быть и общие для обеих величин. В этом случае возникает статистическая зависимость.
Например, если Y зависит от случайных факторов Z1, Z2, V1, V2, а X зависит от случайных факторов Z1, Z2, U1, то между Y и X имеется статистическая зависимость, так как среди случайных факторов есть общие (Z1, Z2).
Статистической называют зависимость, при которой изменение одной из величин влечет изменение распределения другой. В частности, статистическая зависимость проявляется в том, что при изменении одной из величин изменяется среднее значение другой: в этом случае статистическую зависимость называют корреляционной. (Примеры с урожаем зерна и количеством удобрений, ростом и весом человека).
Пусть знач. х велич. Х соотв. сред. знач.велич. У: у1,у2,…,уm. Условным средним  наз.сред. арифмет.знач. велич. У соотв-их знач. велич. X
наз.сред. арифмет.знач. велич. У соотв-их знач. велич. X

Т.обр. усл. сред. явл. функцией от у, т.е. (1) 
Корреляционной зависимостью У от Х наз. функциональн. завис.условного среднего  от Х. Уравнение (1) - называют уравнением регрессии У на Х. Функция f(x) - регрессией У на Х, а ее график - линией регрессии У на Х. Аналогично, м. рассм. корреляционную завис. Х на У, т.е.
от Х. Уравнение (1) - называют уравнением регрессии У на Х. Функция f(x) - регрессией У на Х, а ее график - линией регрессии У на Х. Аналогично, м. рассм. корреляционную завис. Х на У, т.е.  .
.
Пусть Х или У связаны линейной корреляционной зависимостью, т.е. обе линии регрессии прямые. Произведено n испытаний, в результате которых получено следующие пары значений (х1, у1), (х2, у2), …, (хn, уn). Для простоты будем считать, что каждое из значений хi, yi встретилось по одному разу. Наша цель найти уравнение прямой, наилучшим образом приближенной к экспериментальным данным. Т.к. значение не повторяется, то  . Будем искать выборочное уравнение прямой регрессии в виде
. Будем искать выборочное уравнение прямой регрессии в виде  , коэффициент pxy называют выборочным коэффициентом регрессии У на Х. Наша цель провести прямую так, чтобы она была ближе к экспериментальным точкам. Эта задача решается методом наименьших квадратов и заключение в том, что сумма квадратов отклонений должна быть наименьшей
, коэффициент pxy называют выборочным коэффициентом регрессии У на Х. Наша цель провести прямую так, чтобы она была ближе к экспериментальным точкам. Эта задача решается методом наименьших квадратов и заключение в том, что сумма квадратов отклонений должна быть наименьшей  т.е. нужно найти минимум ф-ии
т.е. нужно найти минимум ф-ии

 , т. е.
, т. е.
 ,
, 
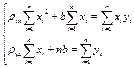


вычтем

Замечание: аналогично можно получить выборочное уравнение прямой регрессии Х на У.
О: Выборочным коэффициентом корреляции наз-ся число

Отсюда

Свойства:
1. | r*|<=1.
2. Если r*=0, и выборочные линии регрессии прямые, Х и У не связаны лин. корреляционной завис. Тогда ур-е прямых регрессии 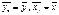 Они м.б. просто коррелируемы, но не линейны. В эт.случ.условное сред.одной велич. не зав. от др.
Они м.б. просто коррелируемы, но не линейны. В эт.случ.условное сред.одной велич. не зав. от др.
3. Если |r*|=1, то наблюдаемое значение величин Х, У связ. лин. функцион. завис., т.е. они все лежат на одной прямой.
4. При увелич. |r*| лин. корреляц. завис-ть стан-ся все сильнее, превращаясь в функцион-ю при |r*|=1.
Вывод: коэффициент корреляции указывает на степень линейной корреляции, силу связи м/у случ. велич., чем он >, тем связь сильнее, чем ближе к нулю, тем слабее.
Если хотя бы одна из линий регрессии не прямая, то корреляция наз-ся нелинейной или криволинейной. Ур-я регрессии м.б. такими:  ;
;  коэф-ты нах-ся с помощью метода наименьших квадратов. Показателем степени связи между величинами служит выборочное корреляционное отношение: ηyx и ηxy. Св-ва: 1) 0≤η≤1. 2)если η=0 то величины не связаны корреляционной завис-ю. 3)при увеличении η связь между величинами становится более тесной. 4)при η=1 величины связаны функц-ой завис-ю.
коэф-ты нах-ся с помощью метода наименьших квадратов. Показателем степени связи между величинами служит выборочное корреляционное отношение: ηyx и ηxy. Св-ва: 1) 0≤η≤1. 2)если η=0 то величины не связаны корреляционной завис-ю. 3)при увеличении η связь между величинами становится более тесной. 4)при η=1 величины связаны функц-ой завис-ю.
Пример: (схематично)
| xi | yi | xi2 | xiyi |
| 1.25 | 1.25 | ||
| 1.5 | 1.4 | 2.25 | 2.1 |
| 1.5 | 4.5 | ||
| 4.5 | 1.75 | 20.25 | 7.875 |
| 2.25 | 11.25 | ||
| 8.15 | 57.5 | 26.97 |
 =15/5=3;
=15/5=3; 
 =8,15/5=1,63;
=8,15/5=1,63;  =26,97/5=5,3;
=26,97/5=5,3;
ρ=…(по ф-лам);  =(по ф-лам)=0,202х+1,024.
=(по ф-лам)=0,202х+1,024.
Date: 2016-02-19; view: 406; Нарушение авторских прав