Тема 5.5 Проекции геометрических тел

Студент должен:

знать: условия и приемы проецирования геометрических тел и предметов на комплексном чертеже. Изображение их в аксонометрических проекциях;

уметь: выполнять проецирование геометрических тел на три плоскости проекций и в аксонометрических проекциях, находить проекции тел, принадлежащих поверхностям геометрических тел.

Определение геометрических тел. Элементы геометрических тел. Проецирование геометрических тел в прямоугольных и аксонометрических проекциях. Определение точек на поверхности геометрических тел.

Практическое занятие. Построение геометрических тел (комплексный чертеж и аксонометрические проекуии).

Литература: 3, с. 89...96; 4, с. 50...73.

Методические указания

Любая деталь состоит из сочетания различных геометрических тел, поэтому надо очень хорошо знать какие бывают геометрические тела, как называются элементы этих тел, и как эти геометрические тела проецируются на три плоскости проекции.

Геометрические тела, поверхность которых ограничена плоскими фигурами, называются многогранниками. Основные элементы призмы приведены на рисунке 25, прямоугольная проекция призмы и ее аксонометрическая проекция - на рисунке 26.

Рисунок 25

Рисунок 26

Пирамидой называется многогранник, у которого одна грань - основание многоугольника, а все боковые грани - треугольники, сходящиеся своими вершинами в одной точке S. На рисунке 27 приведены основные элементы пирамиды и ее прямоугольная проекция.

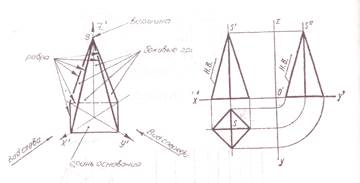
Рисунок 27

Геометрические тела, поверхность которых образована путем вращения замкнутой плоской фигуры вокруг неподвижной оси, называются телами вращения. На рисунке 28 рассмотрены элементы цилиндра и конуса, а на рисунке 29 их прямоугольные проекции.

Рисунок 28

Рисунок 29

Чтобы построить любое геометрическое тело в прямоугольных проекциях, надо выбрать его положение так, чтобы его проекции наиболее наглядно раскрывали его форму.

Шар - поверхность, образованная вращением окружности вокруг собственной оси (рисунок 30).

Рисунок 30

Познакомившись с прямоугольными проекциями геометрических тел, следует помнить, что на их поверхности могут быть даны точки, отрезки прямых и ломаных линий. Если точки или отрезок даны на одной проекции, их надо уметь (на основе анализа знаний по проецированию точек, прямой, плоскости) спроецировать на остальные плоскости проекций.

Вопросы для самоконтроля

1. В какой последовательности строят проекции прямого кругового цилиндра и правильной шестигранной призмы, основания которых расположены на фронтальной плоскости проекций?

2. Какими приемами определяют недостающие проекции точек, лежащих на поверхности конуса, шара к тора?

3. Какие тела называют телами вращения?

4. Чем отличается пирамида от призмы?

5. В виде каких фигур проецируются основные геометрические тела: цилиндр, конус, куб, шар, призма и пирамида?

6. В какой последовательности определяют три проекции точки, заданной на поверхности предмета одной из своих проекций?

7. При каком условии ребро многогранника проецируется в точку? При каком условии - в натуральную величину?

8. При каком условии грань предмета проецируется в линию? Когда в натуральную величину?