Элементы математической статистики

1. Предмет и основные понятия математической статистики.

2. Оценивание. “Хорошие” свойства оценок.

3. Проверка гипотез.

1. Сопоставляя предмет теории вероятности и математической статистики можно сказать, что теория вероятности – это наука о будущем, а математическая статистика – наука о прошлом. Первая из них при известном распределении вероятностей позволяет предсказать вероятность получения того или иного значения случайной переменной. Математическая статистика по известным наблюдениям случайной переменной позволяет определить ее вероятностные характеристики: математическое ожидание, дисперсию, функцию распределения вероятностей и другие.

Классическое определение математической статистики звучит следующим образом:

Математическая статистика – раздел математики, посвященный математическим методам систематизации, обработки и использования статистических данных для научных и практических выводов.

Дадим определение основным понятиям математической статистики: генеральной совокупности и выборки.

Генеральной совокупностью называется совокупность всех мыслимых значений случайной переменной при данном реальном комплексе условий. Иными словами генеральная совокупность – это некая абстракция. Генеральная совокупность описывается статистическими показателями генеральной совокупности или параметрами генеральной совокупности. Если из генеральной совокупности выбрать несколько элементов или произвести несколько испытаний, то мы получим так называемую выборку.

В математической статистике все используемые данные рассматриваются как выборка.

В математической статистике необходимо уметь связывать выборку и воображаемую генеральную совокупность. Это особенно важно в прогнозировании, поскольку прогнозирование означает распространение полученных тенденций на перспективу, т.е. выводов, полученных на основании выборки на генеральную совокупность.

Статистический анализ можно разделить на 2 вида: на описательный анализ и анализ имеющий целью сделать какие-либо выводы.

Статистический анализ

Описательный анализ Анализ получения выводов

Оценивание Проверка гипотез

Под описательным статистическим анализом понимается получение группы сводных показателей, каждый из которых одним числом определяет какое-либо качество генеральной совокупности (среднее арифметическое, медиана, различные отклонения коэффициентов и т.д.).

Оценивание применяется в том случае, если мы заранее не знаем величину параметров генеральной совокупности. В этом случае мы задаем доверительные интервалы для оценивания действительных параметров генеральной совокупности.

В случае, если мы располагаем знаниями относительно параметров генеральной совокупности, то эти сведения могут быть сформулированы в виде гипотезы, которая может быть проверена.

2. Любая случайная переменная обладает характеристиками. Имея какую-то выборку из генеральной совокупности нам надо рассчитать эти характеристики, но прежде чем производить расчеты этих характеристик, необходимо построить формулы для расчета этих оценок. Это и называется оцениванием.

Задача оценивания какой-либо случайной характеристики какой-либо случайной переменной заключается в построении некоторой формулы, основанной на выборочной информации, которая связывает оценочные значения характеристики со значениями выборки X_1, X_2, … X_n. Эта формула называется оценкой:

Числовые значения характеристик, полученных на основе таких формул, также называются оценками. При этом не всякие формулы, связывающие параметры и наблюдения, могут быть оценками. Для успешного ведения статистических исследований оценки должны обладать тремя свойствами:

1. Оценка должна быть не смещенной, т.е. математическое ожидание оценки должно быть равно истинному значению данного параметра для генеральной совокупности. Пусть 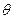оцениваемый параметр, а – это случайная переменная, генерируемая оценочной формулой. Тогда должно выполняться равенство .

2. Оценка должна быть эффективной. Это означает, что оценка должна обладать наименьшей по сравнению с другими оценками дисперсией.

3. Оценка должна быть состоятельной, т.е. при ∞-ом увеличении размера выборки распределение вероятностей оценки должно вырождаться в точку. В дальнейшем оценки, обладающие перечисленными свойствами, мы будем называть «хорошими».

3. Проверка гипотез и основанные на них статистические выводы являются одними из главных задач математической статистики. Разделяют 2 подхода к проверке гипотез. Это классический подход и подход определения уровня вероятности. Иногда при проведении исследований мы располагаем некоторыми предварительными догадками или предположениями относительно величины параметров генеральной совокупности. Располагая этими знаниями, мы можем проверить гипотезу, что наша догадка действительно верна.

Статистическая гипотеза – это рассматриваемое предположение о величине параметра распределения генеральной совокупности. Процесс проверки гипотез базируется на формулировании 2-х гипотез: нулевой и альтернативной, т.е. формируются две конкурирующие гипотезы и проверяется, какая из них является верной.

Нулевая гипотеза, обычно обозначаемая как Н_о - это допущение, которое считается верным до тех пор, пока не будет доказано обратное исходя из результатов статистической проверки.

Альтернативная гипотеза, обычно обозначаемая как Н₁ - это гипотеза, которая принимается, если в результате статистической проверки отвергается нулевая гипотеза.

Точная формулировка гипотезы зависит от того, что конкретно мы хотим установить.

Пример:

Допустим, нам необходимо принять решение относительно добросовестности работы продавцов какого-либо магазина. При контрольной проверке выбран фасованный товар – сахар в килограммовых пакетах.

Рассуждаем следующим образом:

Если выборка из N пакетов имеет вес 1 кг, то работа продавцов удовлетворительна. С точки зрения математической статистики необходимо проверить гипотезу, которая формулируется следующим образом:

«Математическое ожидание веса пакетов для генеральной совокупности равно 1 кг. Принять решение необходимо на основе имеющихся данных, т.е. на основании следующей выборки:

Н_о: М = 1

Н₁: М ≠ 1

Для проверки гипотезы необходимо провести статистическую проверку, состоящую в использовании стандартизированного статистического критерия. Стандартизированный статистический критерий, на основании которого отвергается или принимается гипотеза, вычисляется по данным выборки. Для определения этого критерия необходимо определить математическое ожидание и ее дисперсию по «этой выборке».

«Хорошей» формулой для оценки математического ожидания является:

Рассчитаем дисперсию:

- среднеарифметическое значение переменной Х.

Для проверки гипотезы вычисляют некоторую статистическую величину:

Величина t называется t-статистикой или стандартизированным критерием проверки. Если гипотеза Н_{0 -} верна, то критерий проверки имеет стандартизированное нормальное распределение, или по-другому t-распределение с n-1 степенями свободы.

t-распределение сведено к таблице для различных степеней свободы и вероятностей. Таким образом, если мы зададим достаточно большую вероятность Р=0,98 и по этой вероятности найдем интервал для t по таблице Квантилей, то этот интервал будет областью правдоподобных значений t. И если расчетное значение будет находиться в этом интервале, то у нас есть все основания принять нашу гипотезу Н₀.

В нашем примере

t_{расчетное} =

По таблице находим t_{табличное}:

Таким образом, в нашем примере t ^{рачетное} > t ^{табличное}.

Следовательно, t не попадает в область правдоподобных значений. Следовательно, гипотеза о том, что математическое ожидание весов пакетов равно 1 отвергаем с вероятностью 98%. На обычном языке можно сказать на основании выборки в 98 случаях из 100 средний вес пакетов не будет равняться 1 кг.

Формально классическая процедура проверки гипотезы может быть выражена следующей схемой:

1. Вычисляется оценка вероятностной характеристики по выборке.

2. Выдвигается гипотеза о равенстве оценки, полученной по выборке, истинному значению вероятностной характеристики для всей генеральной совокупности.

3. Вычисляется некоторая статистика по выборочной информации. Эта статистика должна подчиняться некоторому известному закону распределения вероятности.

4. Задается достаточно большая вероятность и находится по таблице распределения интервал для правдоподобных значений вычисленной статистики. Значение заданной вероятности при этом называется статистической надежностью.

5. Если числовое значение расчетной статистики попадает в полученный интервал, то гипотеза принимается. В противном случае – отвергается.

Date: 2016-02-19; view: 494; Нарушение авторских прав