Многофакторное регрессионное уравнение

1. Необходимость использования многофакторных регрессионных уравнений.

2. Оценка коэффициентов регрессии и условия применения метода наименьших квадратов.

3. Показатели адекватности многофакторного регрессионного уравнения.

4. Отбор существенных факторов.

1. Область применения однофакторных регрессионных уравнений ограничена, так как изменения экономических показателей, как правило, объясняются несколькими факторами. В таком случае более приемлемым является математический аппарат многофакторных уравнений. В общем, многофакторное регрессионное уравнение можно записать в виде:

M(y)=f(x₁,x₂,…,x_n)

Линейное многофакторное уравнение записывается в виде:

y=b₀+b₁x₁+b₂x₂+……+b_nx_n+ .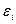

b₁,b₂,…,b_n – коэффициенты регрессии;

b₀ – свободный член регрессии.

2. Коэффициенты регрессии многофакторной модели имеют такой же экономический смысл, что и в однофакторной модели, то есть коэффициент регрессии в многофакторной модели показывает прирост результата (зависимой переменной у), приходящейся на единицу прироста m-го фактора при фиксированных значениях других факторов.

Множественные коэффициенты регрессии, как правило, оцениваются методом наименьших квадратов.

1. Для определения параметров множественной регрессий с k факторами решается система из k+1 уравнений с k+1 неизвестными.

Качество подгонки множественной регрессии оценивается на основе таких же показателей адекватности и тех же критериев, что и в однофакторной модели.

Остаточная дисперсия рассчитывается по формуле:

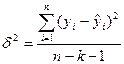
где k – количество факторов.

Коэффициент детерминации рассчитывается по формуле:

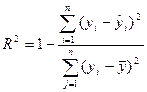
В многофакторном регрессионном уравнении добавление дополнительных объясняющих переменных увеличивает коэффициент детерминации. Следовательно, коэффициент детерминации должен быть скорректирован с учетом числа независимых переменных:

.

F–статистика рассчитывается по формуле:

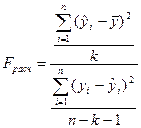
F–критерий проверяется на основе F^таб со степенями свободы k и (n-k-1).

Если F^расч>F^таб, то гипотезу о том, что уравнение несущественно отвергаем.

Особо важное значение для многофакторного регрессионного уравнения имеет t-критерий. На основе t-критерия отбираются существенные факторы в регрессионном уравнении.

На основе для каждого коэффициента регрессии оценивается t-статистика:

, , ……, .

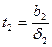Существенность влияния m-го фактора на результат проверяется на основе гипотезы b_m=0. Если гипотеза верна, то t подчиняется t-распределению.

t_табл определяется для заданной вероятности (как правило p=0,95) и степени свободы n-k-1.

При условии, что < гипотеза о том, что b_m=0 отвергается и влияние m-го фактора признается существенным. В противном случае m-ый фактор, а также остальные несущественные факторы исключаются из уравнения, и уравнение регрессии строится заново со всеми вытекающими процедурами проверки адекватности.

При отборе существенных факторов также необходимо иметь в виду, что наличие мультиколлинеарности приводит к искусственному увеличению значений стандартных ошибок , что в свою очередь приводит к уменьшению t-статистики даже для логически существенных связей. В этом случае необходимо применить методы оценивания с учетом мультиколлинеарности.

Date: 2016-02-19; view: 1917; Нарушение авторских прав