Однофакторное регрессионное уравнение

1. Понятие регрессионного уравнения.

2. Метод наименьших квадратов.

3. Проверка адекватности регрессионного уравнения.

3.1. Показатели качества подгонки.

3.2. Проверка различных гипотез относительно регрессионного уравнения.

3.3. «Хорошие» свойства оценок.

3.4. Экономический смысл коэффициентов регрессии.

1. Регрессионное уравнение модели отражает зависимость между экономическими переменными, а именно между одной зависимой (эндогенной) и одной или более независимыми (экзогенными) переменными. Зависимая переменная обозначается через «у», а независимая через «х».

Направление причинно-следственной связи между переменными определяется через предварительное обоснование и включается в модель как гипотеза.

Регрессионный анализ проверяет статистическую состоятельность модели при данной гипотезе.

Регрессионное уравнение может быть однофакторным и многофакторным. В первом случае одна переменная зависит от другой, во втором случае одна переменная зависит от нескольких других.

Регрессионное уравнение, которое отражает зависимость между математическим ожиданием (условным распределением) одной переменной и соответствующим значением другой переменной, называется однофакторным регрессионным уравнением.

В общем виде однофакторное регрессионное уравнение может быть записано в следующем виде:

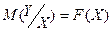₍₁₎

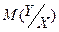- условное математическое ожидание переменной Y при заданном значении переменной X.

Частным случаем однофакторного регрессионного уравнения является линейная модель зависимости, которая записывается следующим образом:

y_i=a+bx_i+ (2)

y_i – объяснимая (зависимая) переменная;

x_i – объясняющая (независимая) переменная;

а – свободный член регрессии или постоянная;

b – коэффициент регрессии, отражает наклон линии, вдоль которой рассеяны данные наблюдения модели. Коэффициент регрессии может быть истолкован как показатель, характеризующий процентное изменение переменной, которым вызвано изменение значения х на единицу.

Если знак перед b положителен, то говорим, что переменные коррелированны положительно, при отрицательном знаке переменные отрицательно коррелированны.

– ошибка или так называемая случайная компонента. Наличие случайной компоненты обусловлено двумя основными причинами:

1. любая регрессионная модель является упрощением действительной, на самом деле есть другие параметры, от которых зависит y_i.

2. присутствуют ошибки измерений.

Необходимо различать кросс-секционную регрессию и регрессию временных рядов.

Кросс-секционная регрессия проверяет связь между переменными в определенный период времени. Например, зависимость между количеством работников предприятия и прибылью, полученной этим предприятием. Чтобы измерить эту связь мы должны собрать данные по численности работников за 1 период (например, год) и данные о размерах прибыли достаточно большого числа предприятий за тот же самый период.

Данные о прибылях компаний соответствовали бы зависимой переменной, а данные о количестве работников были бы независимыми переменными.

При анализе регрессии во временных рядах данные по каждой из переменных собираются в течение следующих друг за другом периодов времени.

Регрессионный анализ временных рядов позволяет установить взаимосвязь между переменными в среднем в течение того периода времени по которому имеются данные. Независимо от того проводится кросс-секционный анализ или анализ временных рядов, основные принципы положения регрессионного анализа остаются те же.

2. Для статистической проверки взаимозависимости между зависимой (у) и независимой (х) переменными, необходимо найти значения а, b, в выражении (2).

Метод оценки этих параметров должен быть таким, чтобы это были «хорошие» оценки.

Метод, используемый чаще других для нахождения параметров регрессионного уравнения и известный как метод наименьших квадратов дает наилучшие линейные несмещенные оценки. Метод называется так потому, что при расчете параметров линии с помощью этого метода минимизируются суммы квадратов значений ошибок .

y

x

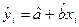
Допустим на графике нанесены наблюдения о совокупных доходах семей (х) и расходах этих же семей на питание (y). Анализируя графики можно сделать следующие выводы:

1. Точки не лежат на одной кривой и можно только провести некоторую линию в непосредственной близости от всех этих точек.

2. Можно сделать допущение, иными словами выдвинуть гипотезу, что доходы и расходы связаны линейной зависимостью, то есть можно построить некоторую прямую 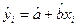, отражающую зависимость между доходами и расходами, при этом значение 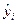назовем теоретически расчетными значениями зависимой переменной, а коэффициенты 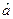и 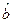– оценочными значениями коэффициентов а и b.

Для того, чтобы теоретическая прямая лежала в непосредственной близости от фактически наблюдаемых у_i необходимо минимизировать сумму квадратов отклонений между фактическими и расчетными значениями.

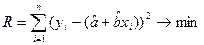
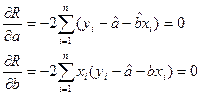
В виде системы:

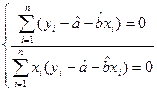
Разрыв скобки получим стандартную форму нормальных уравнений (для краткости опустим индексы у знаков сумм).

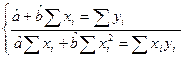
из этой системы находим 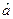и :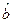

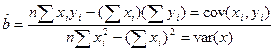
ковариация (cov) показывает тесноту связи

;

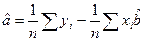n – количество наблюдений.

Так рассчитываются величины регрессии.

Ошибка или случайная компонента находится как разница между расчетными значениями зависимой переменной и фактическими значениями:

.

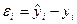3. Адекватность регрессионного уравнения. То есть его соответствие реальному моделироваемому процессу, достоверность его параметров; исследуется с нескольких позиций:

1. Анализируются показатели качества подгонки регрессионного уравнения.

2. Проверяются различные гипотезы относительно параметров регрессионного уравнения.

3. Проверяется выполнение условий для получения «хороших» оценок МНК.

4. Производится содержательный анализ регрессионного уравнения.

3.1. Показатели качества подгонки отражают соотношение расчетных значений зависимой переменной 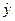с фактическими значениями зависимой переменной у.

Эти показатели как правило основываются на сумме квадратов разности этих показателей:

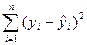
Первый из таких показателей – остаточная дисперсия.

Для однофакторного уравнения однофакторная дисперсия определяется по формуле:

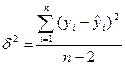
Чем меньше 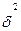, тем лучше регрессионное уравнение, 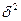- является размерной величиной и сопоставление регрессионных уравнений по нему, отражающих различные переменные невозможно. Показателем, на основании которых возможно сопоставление различных уравнений является коэффициент детерминации, он обозначается :

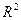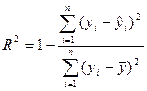, где 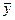- среднеарифметическое значение у.

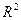принимает значения в интервале [0;1], чем ближе 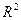к 1, тем лучше качество подгонки регрессионного уравнения. На практике помимо коэффициента детерминации часто используются коэффициенты корреляции, показывающих степень связи между двумя переменными.

Этот показатель также независим от единиц измерения и характеризует силу и направление линейной связи между двумя переменными.

Значение коэффициента находится в интервале от (-1;1).

Если коэффициент близок к -1, то говорят об отрицательной линейной связи. Когда показатель близок к 0, то говорят о линейной независимости двух переменных. Когда показатель близок к 1 – о положительной линейной связи. При анализе коэффициентов корреляции необходимо учитывать, что коэффициент корреляции показывает только силу линейной связи.

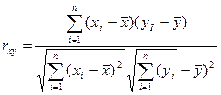
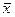- среднеарифметическое значение x.

3.2. Приведенные ранее показатели качества подгонки не позволяют принять статистического решения по пригодности регрессионного уравнения, хотя и дают некоторое представление о качестве подгонки. Такие решения принимают на основе статистических критериев. Одним из таких критериев является F- критерий. Принятие решения на основе F-критерия опирается на общую процедуру проверки гипотезы. После оценки свободного члена регрессии и коэффициента регрессии выдвигается гипотеза о том, что линейная связь между x и y не подтверждается. Отсутствие связи можно изучить на основе отклонений расчетных значений 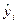от среднеарифметического значения .

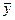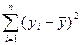
Близкое к 0 значение свидетельствует об отсутствии какой-либо тенденции для y_i в связи с изменениями x. Строгое решение об опровержении линейной связи проверяется на основе F-статистики. Если F^таб<F^расч, то гипотезу об отсутствии линейной связи отвергаем с вероятностью p.

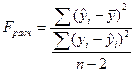
Значения F^таб, берутся из таблицы критических точек распределения F (Фишера-Снедекора) для степеней свободы n₁=1, n₂=n-2.

Отдельно исследуется коэффициент регрессии b. Выдвигается гипотеза о том, что x влияет на y несущественно, то есть y изменяется по каким-то другим причинам, а не в связи с изменением x. Выдвинутая гипотеза равноценна тому, что b равен 0 для генеральной совокупности. Если наша гипотеза верна, то t-статистика подчиняется t-распределению со степенями свободы n-2.

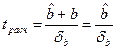, где 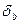- стандартная ошибка коэффициента b рассчитывается по формуле:

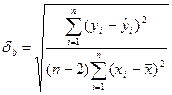
Если t^расч>t^табл, то с заданной вероятностью гипотезу о том, что b=0 отвергаем. t^табл находится по таблице критических точек распределения Стьюдента с заданной вероятностью p b степенью свободы n-2. t-статистика используется также при построении доверительного интервала для коэффициента b.

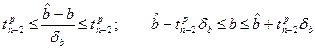
Date: 2016-02-19; view: 2188; Нарушение авторских прав