Непрерывные случайные переменные

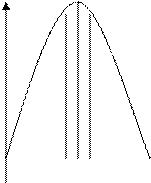
Непрерывные случайные переменные – такие случайные переменные, которые могут принимать бесконечное количество значений (например: скорость, температура, рентабельность активов и т.д.)

Рассмотрим доходность какой-либо ценной бумаги, которая определяется соотношением:

Количество возможных значений доходности может быть бесконечно велико. Изменение цены актива со 105 единиц до 109 единиц даст доходность равную 3,8% или 3,81% или 3, 8095%. В этих обстоятельствах нет никакого смысла в попытках нахождения вероятности значения доходности равной, предположим 3,8%. Имеет смысл только нахождение вероятности того, что случайная переменная примет значение на каком-то определенном интервале, предположим между 3,80% или 3,81%. Таким образом, найти ожидаемую величину непрерывной случайной переменной путем сложения как в случае с дискретными переменными трудно, поскольку пришлось бы искать сумму бесконечного множества вероятностей. Для преодоления этой проблемы мы должны определить непрерывную случайную величину не путем суммирования функций частот вероятностей, а путем интегрирования так называемых функций плотности вероятностей.

, где f(x) – функция плотности вероятности.

p

S=1

 

 

Случайная переменная – такая переменная, поведение которой не определено. Исходя из чего, мы можем только предписывать некоторые вероятности возможным значениям таких переменных.

Основными вероятностными характеристиками случайной переменной являются:

1. распределение вероятностей;

2. математическое ожидание;

3. дисперсия;

 

Date: 2016-02-19; view: 391; Нарушение авторских прав