Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?
Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника
Специальные типы матриц
|
|
1. Симметрическая матрица. Квадратная матрица (m = n) с действительными элементами называется симметрической, если она равна своей транспонированной, т.е. если
, или aij = aji (i,j= 1,2,…, n).
2. Кососимметрическая матрица. Действительная квадратная матрица называется кососимметрической, если
,или aij = – aji (i,j= 1,2,…, n).
Элементы, находящиеся на главной диагонали кососимметрической матрицы, равны нулю, т.е. aij = 0(i= 1,…, n).
3. Комплексно-сопряженная матрица. Если элементы матрицы A комплексные (т.е. aik = αji+jβik, где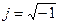 
), то комплексно сопряженная матрица B содержит элементы bik = αji – jβik. Это записывается в форме:
B=A*.
4. Сопряженная матрица. Матрица В, сопряженная по отношению к А является транспонированной и комплексно сопряженной по отношению к А, т.е. равна:
5. Действительная матрица. Матрица А называется действительной, если она равна своей комплексно сопряженной матрице:
A = A*.
6. Мнимая матрица. Матрица А называется мнимой, если она равна своей комплексно сопряженной матрице, взятой со знаком минус:
A = – (A*).
7. Эрмитова матрица. Матрица А называется эрмитовой, если она равна своей сопряженной матрице:
A = (A*)T.
8. Косоэрмитова матрица. Матрица А называется косоэрмитовой, если она равна своей сопряженной матрице, взятой со знаком минус:
A = – (A*)T.
Date: 2016-02-19; view: 473; Нарушение авторских прав