
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Некоторые сведения из теории матриц
|
|
Матрицы необходимы при использовании модели динамики системы в виде переменных состояния, для исследования многомерных систем. Матрица представляет таблицу из m строк и n столбцов:
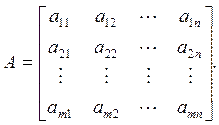
Говорят, что в этом случае размерность (англ. dimention) матрицы равна (m×n). Это можно записать следующим образом:

Основные типы матриц
1. Матрица-столбец(m×1):

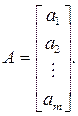
2. Матрица-строка(1×n):
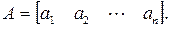
3. Диагональная матрица. Главная диагональ квадратной матрицы состоит из элементов aii. Диагональной матрицей называется квадратная матрица, элементы которой, не лежащие на главной диагонали, равны нулю:
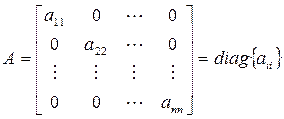 .
.
4. Единичная матрица. Единичной матрицей называется диагональная матрица, диагональные элементы которой равны единице:

5. Нулевая матрица. Матрица, все элементы которой тождественно
равны нулю, называется нулевой матрицей:

6. Транспонированная матрица. Это матрица AT размерности (n×m),в
которой строки и столбцы меняются местами по отношению к исходной матрице А размерности (m×n), т.е. если A = [ aij ], то AT = [ aji ]:
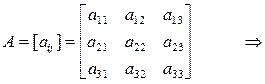
| 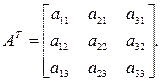
|
Date: 2016-02-19; view: 486; Нарушение авторских прав