Розділ 17. Коректуючі коди

17.1. ОСНОВНІ ПАРАМЕТРИ КОРЕКТУЮЧИХ КОДІВ

Одним із засобів підвищення якості передавання повідомлень дискрет­ними каналами зв'язку із завадами є застосування коректуючих кодів, які дають змогу виявляти та виправляти помилки, що виникають через завади в каналі. Скільки ж помилок може виявити та виправити код? За теоремою Шеннона (див. § 18.2) у разі продуктивності джерела 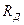, яка менша за пропу­скну здатність каналу , існують коди, що забезпечують безпомил­кове передавання повідомлень. Однак вони дуже складні й поки ще навіть не знайдені, тому запропоновані та використовуються коди, що виявляють і виправляють не всі, а лише частину помилок.

Принцип побудови коректуючих кодів досить простий. Із загальної кількості можливих кодових комбінацій довжиною п символів й обсягом т для передавання дискретних повідомлень використовуються не всі, а тільки необхід­на кількість кодових комбінацій , що дорівнює обсягу первинного алфавіту (звичайно ). Кодові комбінації, що використовуються, названі дозволени­ми. Решта кодових комбінацій є забороненими, тобто вони не можуть передаватись каналами зв'язку, і їх поява на приймальному кінці свідчить про наявність помилок. Таким чином, будь-який коректуючий код є надлишковим або надмірним кодом (має зайві, що не використовуються, кодові комбінації).

Коректуючий код характеризується такими параметрами, як коректуюча здатність, хеммінгова віддаль, кодова віддаль, вага кодової комбінації та відносна швидкість коду.

Коректуюча здатність коду - це гарантована кількість (кратність) по­милок у кодовій комбінації, що виявляються або виправляються заданим кодом. Позначається кратність помилок так: код виявляє в кодовій комбінації помилок, виправляє помилок. Цілком ясно, що чим біль­шими є кратності і , тим кращим є код.

Хеммінгова віддаль показує міру різниці між -ю -ю кодовими комбі­націями. Для будь-яких двох двійкових кодових комбінацій однакової довжини кодова віддаль дорівнює числу незбіжних у них розрядів. Так, наведені нижче кодові комбінації (для зручності порівняння вони написані одна попід другою)

незбіжні в трьох розрядах (позначені пунктиром). І тому хеммінгова віддаль . Математично хеммінгова віддаль підраховується як кількість одиниць

у сумі за модулем два (mod 2) цих двох кодових комбінацій. Нагадаємо правило додавання за модулем два: ; ; ; ( - знак додавання за mod 2).

Кодова віддаль - це щонайменша хеммінгова віддаль для заданого коду. Перебираючи всі можливі пари дозволених кодових комбінацій і розрахову­ючи для них , знаходимо щонайменше значення . Це і є кодова віддаль , яка повністю характеризує коректуючу здатність коду.

Вага кодової комбінації показує кількість ненульових символів (тобто кількість одиниць для двійкового коду) в кодовій комбінації.

Відносна швидкість коду показує відносне число дозволених кодових комбінацій у коді і розраховується за формулою

. (19.1)

17.2. ПРИНЦИПИ ПОБУДОВИ КОРЕКТУЮЧИХ КОДІВ

Схема ввімкнення кодера і декодера коректуючого коду в систему пере­дачі дискретних повідомлень двійковими кодами показана на рис. 19.1. До входу кодера надходить послідовність двійкових символів 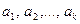пер­винних ненадлишкових кодових комбінацій a_i згідно зі знаками повідомлен­ня. У процесі кодування кодові комбінації a_i довжиною перетворюються в дозволені кодові комбінації b_i довжиною із символами , тобто кодер додає в первинні ненадлишкові кодові комбі­нації додаткових символів, що називаються перевірними. Відносна швидкість цього надлишкового коду обчислюється за формулою (19.1), що з урахуванням співвідношень та набуває вигляду

Прийнята кодова комбінація може в будь-якому символі відрізнятися від переданої комбінації а,- внаслідок помилок, що виникають на виході дискретного каналу зв'язку, тому кожний з її символів позначено "шляпкою". У декодері в разі надлишкового кодування з'являється можливість виявлення та виправлення помилок. Для реалізації цієї можливості, як зазначено вище (див. § 19.1), усі кодові комбінації корек­туючого коду розподіляються на дозволені та заборонені. У кодері формую­ться тільки дозволені кодові комбінації. Перехід їх у заборонені через поми­лки в каналі є необхідною умовою для виявлення та виправлення помилок, тому головна задача побудови будь-якого коректуючого коду - розподіл усіх кодових комбінацій на дозволених і заборонених так, щоб забезпечити необхідну коректуючу здатність коду. В цілому це досить скла­дна задача, що розв'язується різними методами залежно від вимог до деко­дера (потрібно виявляти чи виправляти помилки).

Декодування з виявленням помилок. Методика виявлення помилок під час декодування досить проста: прийнята кодова комбінація порівнюєть­ся по черзі з усіма дозволеними, і якщо вона не збігається ні з однією з них, то виноситься рішення про наявність помилок.

Для виявлення помилок певної кратності кодова віддаль між будь-якими дозволеними кодовими комбінаціями має бути достатньою для того, щоб у разі зміни одного чи кількох символів у них через помилки не виникала знову дозволена кодова комбінація. Отже, для виявлення помилок кодова віддаль має бути хоч на одиницю більшою за кратність помилок , що виявляються кодом, тобто

. (19.3)

Нагадаємо, що помилка кратності веде до зміни в кодовій комбінації символів, тобто хеммінгова віддаль між початковою і кодовою комбінацією з помилками дорівнює .

Декодування з виправленням помилок. У кодах із виправленням по­милок пред'являються більш жорсткі вимоги до кодової віддалі між дозволе­ними кодовими комбінаціями. Виправлення помилок можливе також тільки в тому випадку, коли передана дозволена кодова комбінація через помилки переходить у заборонену. Рішення про те, яка кодова комбінація передава­лась, приймається в декодері на основі порівняння прийнятої забороненої кодової комбінації з усіма дозволеними. Прийнята заборонена кодова комбінація ототожнюється з тією дозволеною, до якої вона більш за все подібна, тобто з тією, від якої вона відрізняється меншим числом символів. За цим правилом, для виправлення помилок кратністю заборонена кодова комбінація, набута через помилки, має залишатись ближчою до переданої справжньої дозволеної, ніж до будь-якої іншої дозволеної кодової комбінації. Наведене вище правило виконується за такої умови

. (19.4)

Співвідношення (19.3) та (19.4) є основними для визначення коректуючої здатності коду, оскільки вони дають змогу при заданій кодовій віддалі знайти кратність помилок, що виявляються та виправляються у декодері. Наприклад, якщо "сусідні" дозволені кодові комбінації мають кодову віддаль , то в разі помилок кратності чотири і менше будь-яка дозволена кодова комбінація не може перейти в іншу дозволену, і наявність помилок легко виявити. Виправлятись будуть тільки одно- і двократні помилки, тому що вже при трьох помилках набута заборонена кодова комбінація буде ближче до іншої дозволеної. Сказа­не ілюструється рис. 19.2.

Умовно віддаль між трьома до­зволеними кодовими комбінаціями b₁, b₂, b₃ показана прямими лініями, на яких через інтервал від­кладені заборонені кодові комбіна­ції, що відрізняються в 1 - 4 симво­лах від дозволених. Штрихами обведена зона, що оточує кожну дозволену кодову комбінацію b_i. Радіус зони вибрано таким, що дорівнює , і до цієї зони попадають такі заборонені кодові комбінації, які знаходяться ближче до дозволеної в центрі цієї зони, ніж до дозволеної комбінації в іншій зоні. Під час декодування кодові комбінації, що знаходяться в будь-якій зоні, ототожнюються з дозволеною кодовою комбінацією цієї зони. Трикратна помилка, наприклад у b₁, переводить її в зону комбінації b₂ (на рис. 19.2 цей перехід показаний стрілкою), і під час декодування буде прийняте рішення, що передавалась комбінація Ь₂ (помилки не виправлені).

Отже, задача утворення коду з необхідною коректуючою здатністю зво­диться до задачі формування в кодері дозволених кодових комбінацій із необхідною кодовою віддаллю .

Кількість перевірних символів коректуючого коду. Точної формули для розрахунків кількості додаткових перевірних символів для заданого числа інформаційних символів і кодової віддалі досі ще не знайдено. Встановлені лише нижня і верхня оцінки (межі) цієї кількості, які, відповід­но, означають мінімальну і максимальну кількості перевірних сим­волів у кодовій комбінації коректуючого коду. Для двійкових кодів ці межі можна розрахувати за формулами

; (19.5)

, (19.6)

де - число сполучень із по . Для верхня і нижня межі зливаються, і визначене за формулами (19.5) чи (19.6) значення є точним.

Розрахунками на ЕОМ встановлено, що формула (19.6), яку називають межею Варшамова-Гільберта, дає дещо завищені, але дуже близькі до точних значення. У табл. 19.1 наведені дані розрахунків за формулою (19.6) для числа інформаційних символів у кодовій комбінації і кодовій віддалі 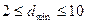. Із таблиці випливають дуже важливі для практичної побудови коректуючих кодів висновки:

1) при зростанні кодової віддалі і, відповідно, коректуючої здатності ко­ду різко підвищується кількість перевірних символів, значно зменшується відносна швидкість коду (на один інформаційний символ потрібно два-п'ять перевірних);

2) для утворення доброго коректуючого коду (виправляє дві і більше по­милок) при відносній швидкості його кодова комбінація повинна мати кілька десятків інформаційних символів (див. приклад 19.3).

19.1. Кількість перевірних символів у кодовій комбінації (верхня межа Варшамова-Гільберта)

Кількість інформаційних символів

і

ІЗ

ЗО

Значна кількість інформаційних символів у кодовій комбінації доброго коректуючого коду накладає технічні труднощі на наведену вище процедуру декодування - порівняння прийнятої кодової комбінації з усіма дозволеними. Це добре показує приклад 19.4.

Як видно з прикладу 19.4, задача декодування звичайним перебором і порівнянням не під силу навіть сучасним ЕОМ (і, можливо, ЕОМ майбутньо­го), тому на практиці набули розповсюдження такі методи кодування й декодування, що не потребують перебору та порівняння і мають допустиму складність при реалізації.

Синдромне декодування. Синдромний метод декодування базується на простому правилі: для виправлення помилок необхідно знати не лише факт їх існування, але й місцезнаходження. Тому під синдромом коду розуміють контрольне число , що свідчить про наявність помилок і їх розташування (конфігурацію) у кодовій комбінації. Відзначимо, що у двійковому коді синдром записується у двійковій системі числення, тобто його розряди приймають значення 0 або 1. Нульовий синдром указує на те, що кодова комбінація є дозволеною, тобто виявлених помилок нема. Ненульовому синдрому відповідає певне (визначене раніше) розмі­щення помилок, які й виправляються.

Чи досить знання синдрому для виправлення помилок? У загальному ви­падку - ні. Необхідно ще знати, на які символи потрібно замінити помилково прийняті. Проте для двійкових кодів виправлення помилок провадиться єди­ним способом - інверсією символів (0 замінюється на 1 і, навпаки, 1 - на 0). Тому знання синдрому є необхідною і достатньою умовою для виправлення помилок у двійкових кодах. Таким чином, синдромне декодування двійкових кодів зводиться до пошуку тим чи іншим способом синдрому, за яким вияв­ляються або виправляються помилки. Десятки запропонованих до цього часу коректуючих кодів і відрізняються саме методами формування перевірних символів та знаходження синдрому при декодуванні.

Класифікація коректуючих кодів. Згідно з основними параметрами й ме­тодами кодування коректуючі коди можна поділити на блокові та неперервні.

Блокові коди характерні тим, що послідовність інформаційних символів поділяється на блоки довжиною символів. Операції кодування і декодування кожного блоку проводяться окремо і незалежно. Особливістю неперервних кодів є те, що послідовність інформаційних символів не поділяється на блоки, а перевірні символи розміщуються за певним правилом між інформаційними.

Різновидом як блокових, так і неперервних кодів є роздільні та нерозді­льні коди. У роздільних кодах завади можна визначити, де інформаційні та де перевірні символи. У нероздільних кодах це неможливо.

Роздільні коди, у свою чергу, можуть бути систематичними або несисте­матичними. Систематичними називаються коди, в яких сума за модулем два двох дозволених кодових комбінацій дає знову дозволену кодову комбіна­цію. Крім того, у систематичному коді інформаційні символи, як правило, не міняються при кодуванні і займають певні раніше визначені місця. Перевірні символи знаходяться як лінійна комбінація інформаційних. Звідси і друга назва систематичних кодів -лінійні. Для систематичних кодів використовує­ться позначення – 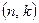-код, де, як і раніше, - загальна кількість символів (довжина) кодової комбінації; - кількість інформаційних символів у ній. Для несистематичних кодів наведені вище правила не виконуються.

Правила (алгоритми) побудови деяких двійкових коректуючих кодів, що найчастіше вживаються, наведені в § 17.3 - 17.5. Схемна реалізація кодера та декодера цих кодів здійснюється на базі логічних елементів обчислювальної техніки і розглядається в спеціальних дисциплінах (телеграфія і передача даних, імпульсна техніка).

17.3. КОДИ З ПОСТІЙНОЮ ВАГОЮ

Усі дозволені кодові комбінації двійкового коду з постійною вагою ма­ють однакову кількість одиниць. Нагадаємо (див. § 19.1), що вага коду - кількість одиниць у двійковій кодовій комбінації. Коди з постійною вагою відносяться до класу блокових нероздільних кодів; тому що в них неможливо знайти окремо інформаційні та перевірні символи.

Типовим прикладом коду з постійною вагою є семирозрядний телеграфний код № З (МТК-3), рекомендований Міжнародним консультативним комітетом із телефонії й телеграфії (МККТТ) для використання в системах зі зворотним зв'язком із метою виявлення помилок. Вага коду дорівнює трьом, отже, кожна дозволена кодова комбінація має три одиниці й чотири нулі. У МТК-3 з усієї кількості кодових комбінацій М=128 дозволеними є тільки .

Знаходження помилок при декодуванні кодів із постійною вагою зводиться до визначення їх ваги (підрахунку кількості одиниць). Наприклад, легко знайти, що із трьох прийнятих кодових комбінацій коду МТК-3: 1011000, 1101010, 0101010 - помилки є в другій, оскільки її вага 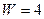. Цей код виявляє всі помилки непарної кратності та частину помилок парної кратності. Не виявляються тільки так звані помилки суміщення, що зберігають без зміни вагу комбінації. Характерним для помилок суміщення є те, що кількість помилок одиниць завжди дорівнює кількості помилок нулів. Тому коди з постійною вагою більш ефективні в каналах, де ймовірність помилок суміщення мала.

17.4. КОД ІЗ ПАРНИМ ЧИСЛОМ ОДИНИЦЬ

Це систематичний 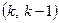-код, в якому основним правилом при коду­ванні й декодуванні є перевірка на парність. Кодова віддаль для цього коду . Тому, згідно з правилом (19.3), код завжди виявляє однократні помилки. Дозволені кодові комбінації цього коду при будь-якому числі інформаційних символів мають один перевірний. Розміщення перевірного символу в кодовій комбінації не має значення. Звичайно його ставлять після інформаційних символів. Значення перевірного символу розраховується з умовою, що загальна кількість одиниць в утвореній таким чином дозволеній кодовій комбінації була парною (звідси і назва коду). Математично парність означає, що сума за модулем два всіх символів кодової комбінації дорівнює нулю (правило додавання за модулем два див. у § 19.2).

Якщо розряди кодових комбінацій пронумерувати справа наліво і симво­ли в цих розрядах позначити для ненадлишкового коду а для надлишкового коректуючого то описану вище процедуру формування дозволеної кодової комбінації і синдрому можна записати так:

, для (19.7)

і синдром

, (19.8)

де, як і раніше, значок означає додавання за модулем два. У виразах (19.7) перший показує, що інформаційні символи при кодуванні не змінюються, другий - надає правило формування перевірного символу. Формула (19.8) є правилом знаходження синдрому (контрольної суми) цього коду як результат перевірки кодової комбінації на парність (синдром має тільки один розряд).

У разі будь-якої однократної помилки (байдуже, в інформаційному чи перевірному символах) синдром 8 не дорівнює нулю, і тим самим помилка виявляється.

Порушення парності має місце в разі появи не тільки однократних поми­лок, але й помилок непарної кратності, що дає можливість їх виявляти. Поява парних помилок не міняє контрольної суми (19.8), тому такі помилки кодом із парним числом одиниць не виявляються. До переваг розглянутого коду слід віднести простоту кодера і декодера, малу надлишковість. Але цей код має низьку коректуючу здатність, що обмежує його використання.

17.5. ЦИКЛІЧНІ КОДИ

Циклічні коди належать до систематичних кодів і назву дістали внаслі­док певної своєї властивості: циклічне переставлення дозволеної кодової комбінації дає знову дозволену. При циклічному переставленні символи кодової комбінації переміщуються зліва направо на один розряд, а крайній правий символ переноситься на місце крайнього лівого. Наприклад, із циклічним переставленням дістаємо .

У теорії циклічних кодів усі перетворення кодових комбінацій виконую­ться у вигляді математичних операцій над поліномами (многочленами). Для цього кодові комбінації зображуються у формі поліномів. Так, кодова комбі­нація при записується у вигляді

Запис полінома, як правило, спрощують, випускаючи співмножники і складові, до яких входить . Наприклад, кодова комбінація зображується поліномом , а комбінація поліномом .

Операції над поліномами. При формуванні кодових комбінацій циклічного коду і знахо­дженні синдрому використовуються такі математичні операції, як додавання, віднімання, множення і ділення поліномів. Вони виконуються за звичайними арифметичними правилами, тільки додавання виконується за модулем два. а віднімання замінюється додаванням. Покажемо виконання цих операцій на конкретних прикладах раніше наведених поліномів і :

, оскільки ;

;

Формування дозволених кодових комбінацій. Дозволені кодові комбі­нації циклічного коду мають важливу ознаку: всі вони без остачі діляться на поліном , що називається породжуючим або твірним. Із цієї властивості випливає простий метод формування дозволених кодових комбінацій - множення комбінацій ненадлишкового коду на породжуючий поліном:

. (19.9)

У теорії циклічних кодів доводиться, що породжуючими поліномами можуть бути тільки поліноми, які є дільниками двочлена . Знайдені за допомогою ЕОМ породжуючі поліноми зведені у великі таблиці. Деякі із цих поліномів наведені в табл. 19.2. Слід відзначити, що із підвищенням макси­мального степеня породжуючих поліномів різко зростає їх число. Так, при є всього два поліноми, а при їх вже кілька десятків.

Date: 2016-02-19; view: 1593; Нарушение авторских прав