Продуктивність джерел повідомлень

Вид повідомлення (первинних сигналів)	Характер повідомлень	Параметри АЦП	Продуктивність, біт/с
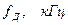
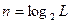
Телеграфне 50 Бод	Дискретні	-	-	30-50
Передача даних 2400 Бод	«	-	-
Розмовне	Неперервні
Звукове мовлення:
першого класу	«			240 000
вищого класу	«
Факсимільне при швидкості 120рядків/с:
напівтонове	«	2,93		11 720
штрихове	Дискретні	-	-	2 930
апаратури "Газета-2"	«	-	-	360 000
Відео (телевізійне)	Неперервні			216 Х 106

16.2. ІНФОРМАЦІЙНІ ХАРАКТЕРИСТИКИ КАНАЛІВ ЗВ'ЯЗКУ

Швидкість передавання інформації каналами зв'язку. Під швидкістю передавання інформації розуміють середню кількість інформації, що надхо­дить із виходу каналу за одиницю часу; вимірюється у дв.од./с або біт/с.

Цілком ясно, що в ідеальному каналі без завад і спотворень кількість прийнятої інформації тотожно дорівнює кількості переданої інформації. Тому швидкість передавання інформації 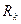ідеальним каналом обчислюється аналогічно продуктивності джерела за формулами (18.6) чи (18.8), виходячи з інформаційних параметрів первинного сигналу.

Наявність у каналі завад призводить до спотворення прийнятих сигналів, через те ми не можемо визначити з повною достовірністю, яке саме повідом­лення було передане. Тому можна стверджувати, що в каналі зв'язку із завадами виникають втрати інформації. Це підтверджується хоча б таким усім відомим фактом: розмовляючи по телефону при наявності завад абонент просить повторити сказане, тому що він не все почув і зрозумів, а це означає, що деяка частина інформації не дійшла до споживача та втрачена в каналі.

Отже, розраховуючи швидкість передавання інформації в каналах із за­вадами, необхідно враховувати втрати, і тоді швидкість передавання інформації дискретним каналом

, (18.9)

неперервним каналом

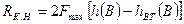, (18.10)

де 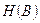- ентропія дискретного первинного сигналу; 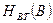, 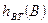- ентропія втрат інформації в каналі відповідно для дискретного і неперервного пер­винних сигналів; 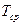- середня тривалість дискретного первинного сигналу; - максимальна частота спектра неперервного первинного сигналу ; 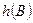- диференціальна ентропія первинного неперервного сигналу.

Втрати інформації, звичайно, залежать від якості передавання сигналів, тобто від імовірності помилок сигналів у дискретному каналі та відношення сигнал-завада в неперервному каналі. Зрозуміло, що втрати інформації зменшуються, якщо якість передавання підвищується. Дослідження показа­ли, що при ймовірності помилок у каналі, меншій за 10^-3, і відношенні сигнал-завада, більшій за 20 дБ, втрати інформації незначні - долі відсотка від переданої інформації. Тому для практичних розрахунків швидкості передавання інформації в каналах із високою якістю втратами інформації можна нехтувати.

Пропускна здатність каналів. Найбільше значення швидкості переда­вання інформації каналом зв'язку при заданих обмеженнях називають пропу­скною здатністю каналу; вимірюється у дв.од./с або біт/с і визначається за такою формулою:

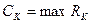. (18.11)

Під заданими обмеженнями слід розуміти тип канапу (дискретний чи не­перервний), характеристики каналу, сигналів та завад. Нагадаємо, що канал називають дискретним, якщо на вході та виході його діють дискретні сигна­ли; неперервним називають канал, на вході та виході якого неперервні сигнали.

Пропускна здатність дискретного каналу 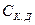, яким передається т дис­кретних сигналів, обчислюється за формулою

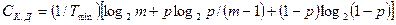, (18.12)

де - мінімальна тривалість сигналу; 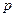- імовірність помилки сигналів у каналі. З виразу (18.12) випливають дуже важливі окремі випадки:

пропускна здатність дискретного каналу без завад

;

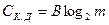пропускна здатність двійкового каналу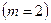

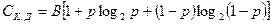, (18.13)

де - швидкість модуляції, Бод.

Залежність від імовірності помилки 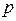, обчислена за формулою (18.13), зображена на рис. 18.1. Якщо 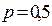, пропускна здатність двійкового каналу 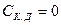, тобто таким каналом інформацію неможливо передавати. Цей випадок називають обривом каналу. Фізично це значить, що ймовірність помилки 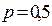виникає в каналі із зава­дами і в разі відсутності сигналу. Проте якщо 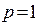(кожний символ помилковий), пропускна здатність така сама, що й у каналі без помилок. Цей, на перший погляд, дивний факт пояснюється тим, що при 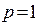відбувається безпомилкове приймання символів у "негативі", тобто досить замінити 0 на 1 та 1 на 0, щоб правильно відновити повідомлення. Втрат інформації при цьому нема.

Для неперервного гауссового каналу з постійними параметрами (завади мають гауссовий розподіл імовірності) максимальна швидкість передавання інформації досягається за умови, що і сигнал має гауссовий розподіл імовірності миттєвих значень при обмеженій середній потужності. Розрахун­кова формула пропускної здатності неперервного гауссового каналу одержа­на в 1948 р. К.Шенноном і носить його ім'я (формула Шеннона):

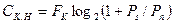, (18.14)

де - ширина смуги частот каналу; 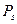, 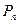- середні потужності відповідно сигналу і завади у смузі частот каналу.

З формули (18.14) випливає, що пропускна здатність гауссового каналу про­порційна ширині смуги частот каналу та відношенню сигнал-завада і зростає в разі їх підвищення. Формула (18.14) указує на можливість обміну ширини смуги частот каналу на потужність сигналу при тій самій пропускній здатності. Проте в разі безмежного збільшення ширини смуги частот каналу неможливо також безмежно підвищувати пропускну здатність каналу. Зі зростанням підвищу­ється потужність завад, тому що для завад типу білого шуму зі спектральною густиною потужності 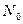(див. приклад 2.9) потужність завад Тоді з формули (18.14), ураховуючи, що 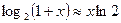, одержимо

іншими словами, максимальне значення, до якого наближається пропускна здатність неперервного гауссового каналу зі зростанням ширини смуги частот каналу, пропорційне відношенню середньої потужності сигналу 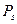і спектральної густини потужності завади .

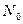Основна теорема кодування Шеннона для каналу із завадами. Про­пускна здатність каналу характеризує потенційні можливості передавання інформації. Ці можливості розкриті у фундаментальній теоремі теорії інформації, відомій як основна теорема кодування Шеннона. Формулювання її для дискретного каналу таке: якщо продуктивність джерела повідомлень 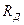менша за пропускну здатність каналу , тобто

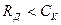, (18.15)

то існують способи кодування (перетворення повідомлення в сигнал на вході каналу) та декодування (перетворення сигналу в повідомлення на виході каналу), при яких імовірність помилки декодування може бути безмежно малою. Якщо ж 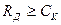, то таких способів кодування та декодування не існує. Для неперервних каналів формулювання теореми таке саме, але під помил­кою декодування слід розуміти середньоквадратичну похибку (різницю), що визначається за формулою (1.8).

Таким чином, згідно з теоремою Шеннона, помилки в каналі не с пере­шкодою для безпомилкового передавання інформації. Помилки дещо змен­шують пропускну здатність каналу (див. приклад 18.4), але за умови виконання нерівності (18.15) належними способами кодування та декодування їх усі можна виправити. Проте в доведенні теореми, яке тут через складність не наводиться, не указується конкретний код, що виправляє всі помилки. Дово­диться тільки, що код повинен мати велику довжину, тобто кодувати необ­хідно не окремі літери, а цілі слова і навіть фрази. Тому коди, що виправля­ють усі помилки, дуже складні та поки що не знайдені.

Пропускна здатність каналу як межа швидкості безпомилкового переда­вання інформації є однією з основних характеристик будь-якого каналу. Для типових неперервних каналів багатоканального зв'язку основні технічні характеристики та пропускна здатність, обчислена за формулою Шеннона (18.14), наведені в табл. 18.2. Апаратура цифрових систем багатоканального зв'язку забезпечує створення цифрових каналів з імовірністю помилки символів 10^-5 - 10^-8 і такими градаціями швидкості, кбіт/с: основний цифро­вий канал - 64; субпервинний канал - 480: первинний тракт - 2048; вторин­ний тракт - 8448; третинний тракт - 34 368; четверинний тракт - 139 264.

Date: 2016-02-19; view: 580; Нарушение авторских прав