
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Імовірність помилки при оптимальному прийманні дискретних сигналів
|
|
| Дискретний сигнал | Когерентне приймання | Некогерентне приймання |
| АМ-2 | 
| 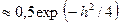
|
| ЧМ-2 | 
| 
|
| ФМ-2 | 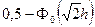
| - |
| ВФМ-2 | 
| 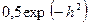
|
Формулами з табл. 16.2 для ймовірності помилки користуються під час розв'язування основних задач аналізу та синтезу оптимальних демодуляторів: обчислення завадостійкості приймання для заданих сигналів і завад та, навпаки, визначення необхідних характеристик сигналів і завад за заданою завадостійкістю.
 Порівняння завадостійкості приймання дискретних сигналів. Порівнюючи завадостійкість, необхідно дати відповідь на запитання: "Які сигнали, методи приймання кращі за завадостійкістю і на скільки?" Звичайно завадостійкість порівнюють не за ймовірністю помилки через досить значні її зміни, а за енергетичним виграшем. Під енергетичним виграшем
Порівняння завадостійкості приймання дискретних сигналів. Порівнюючи завадостійкість, необхідно дати відповідь на запитання: "Які сигнали, методи приймання кращі за завадостійкістю і на скільки?" Звичайно завадостійкість порівнюють не за ймовірністю помилки через досить значні її зміни, а за енергетичним виграшем. Під енергетичним виграшем  , дБ, розуміють різницю в енергіях сигналів при однаковій імовірності помилки для різних сигналів, способів приймання, кодування тощо, тобто
, дБ, розуміють різницю в енергіях сигналів при однаковій імовірності помилки для різних сигналів, способів приймання, кодування тощо, тобто
 для
для  ,
,  . (16.6)
. (16.6)
Якщо  , то це вже не виграш, а енергетичні втрати. Значення енергій для розрахунків
, то це вже не виграш, а енергетичні втрати. Значення енергій для розрахунків  , часто дістають не за формулами ймовірності помилок, а за графічними залежностями
, часто дістають не за формулами ймовірності помилок, а за графічними залежностями 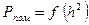 , які дають більш наочне уявлення про завадостійкість.
, які дають більш наочне уявлення про завадостійкість.
Як приклад на рис. 16.4 зображені залежності 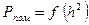 для оптимального приймання двійкових сигналів, що побудовані за формулами з табл. 16.2. Імовірність помилки на графіках для зручності відкладена в логарифмічному масштабі. З рис. 16.4 чітко видно, що найбільшу завадостійкість має система із сигналами ФМ-2, найменшу - із сигналами АМ-2. Якщо обчислити
для оптимального приймання двійкових сигналів, що побудовані за формулами з табл. 16.2. Імовірність помилки на графіках для зручності відкладена в логарифмічному масштабі. З рис. 16.4 чітко видно, що найбільшу завадостійкість має система із сигналами ФМ-2, найменшу - із сигналами АМ-2. Якщо обчислити  за формулою (16.6), дістаємо, що система з протилежними сигналами ФМ-2 дає енергетичний виграш на З дБ (або у два рази) порівняно з ортогональними сигналами ЧМ-2 та на 6 дБ (або в чотири рази) порівняно із сигналами АМ-2.
за формулою (16.6), дістаємо, що система з протилежними сигналами ФМ-2 дає енергетичний виграш на З дБ (або у два рази) порівняно з ортогональними сигналами ЧМ-2 та на 6 дБ (або в чотири рази) порівняно із сигналами АМ-2.
З рис. 16.4 випливає, що енергетичні втрати некогерентного приймання незначні - 1-2 дБ, тому під час практичного виконання приймачів сигналів АМ-2 та ЧМ-2 перевага надається некогерентному прийманню.
14.4. ОПТИМАЛЬНЕ ПРИЙМАННЯ НЕПЕРЕРВНИХ СИГНАЛІВ
Критерій оптимальності. Задача приймання неперервних модульованих сигналів істотно відрізняється від задачі приймання дискретних сигналів. Тут у результаті оброблення сигналів у приймачі необхідно не тільки подавити заваду, але й відновити переданий сигнал. Спотворення його форми мають бути щонайменшими.
Таким чином, якщо за основу прийняти кількісну міру завадостійкості передавання неперервних сигналів, що визначається за формулою (16.2), то критерієм оптимальності буде мінімум середньоквадратичної різниці (відхилення) між прийнятим  та переданим
та переданим 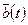 первинними сигналами:
первинними сигналами:
 . (16.7)
. (16.7)
 |
Цей критерій запропонований також В. О. Котельниковим і є найбільш загальним. Він враховує не тільки завади, а й спотворення прийнятих сигналів.
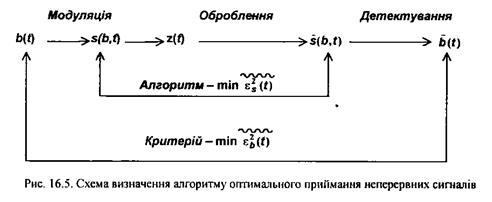
Алгоритм оптимального приймання. Правило (алгоритм) роботи оптимального приймача, що забезпечить виконання критерію за формулою (16.7), можна знайти із розглядання процесів перетворення первинних сигналів при їх передаванні в системі зв'язку (див. § 1.1 та рис. 16.5).
Згідно з критерієм оптимальності, визначеним за формулою (16.7), необхідно забезпечити мінімальну різницю (у середньому) між прийнятим та переданим первинними сигналами. Якщо вважати, що операції модуляції та детектування ідеальні і не вносять спотворень, то з рис. 16.5 випливає, що мінімум середньоквадратичної різниці між первинними сигналами забезпечується у разі мінімальної різниці (у середньому) між прийнятим  та переданим
та переданим  модульованими сигналами. Отже, алгоритмом роботи оптимального приймача (демодулятора) неперервних сигналів можна вважати рівність
модульованими сигналами. Отже, алгоритмом роботи оптимального приймача (демодулятора) неперервних сигналів можна вважати рівність
 . (16.8)
. (16.8)
Таким чином, оптимальний приймач неперервних сигналів згідно з алгоритмом (16.8) має забезпечувати мінімум середньоквадратичної різниці (відхилення) прийнятого модульованого сигналу від переданого. У разі ідеальних модулятора та детектора такий приймач буде відновлювати первинний сигнал  з щонайменшим відхиленням від переданого.
з щонайменшим відхиленням від переданого.
 |
Структурна схема оптимального приймача. Забезпечити оброблення прийнятого сигналу
 так, щоб дістати
так, щоб дістати 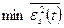 , можна за допомогою оптимального лінійного фільтра Колмогорова-Вінера. Цей фільтр саме і забезпечує найкраще подавлення завад при мінімальних спотвореннях форми сигналу. Проте лінійний фільтр за алгоритмом (16.8) є оптимальним для модульованого сигналу
, можна за допомогою оптимального лінійного фільтра Колмогорова-Вінера. Цей фільтр саме і забезпечує найкраще подавлення завад при мінімальних спотвореннях форми сигналу. Проте лінійний фільтр за алгоритмом (16.8) є оптимальним для модульованого сигналу  , а не для первинного. Він здійснює оптимальне додетекторне оброблення. Отже, після фільтра має бути ввімкнутий ідеальний детектор для заданої модуляції. Тому узагальнена структурна схема приймача неперервних сигналів буде мати вигляд, який подано на рис. 16.6. Вона повністю еквівалентна схемі оброблення неперервних сигналів фільтрами. Різниця тільки в тому, що для забезпечення щонайкращого (оптимального) оброблення необхідні оптимальний фільтр та ідеальний детектор.
, а не для первинного. Він здійснює оптимальне додетекторне оброблення. Отже, після фільтра має бути ввімкнутий ідеальний детектор для заданої модуляції. Тому узагальнена структурна схема приймача неперервних сигналів буде мати вигляд, який подано на рис. 16.6. Вона повністю еквівалентна схемі оброблення неперервних сигналів фільтрами. Різниця тільки в тому, що для забезпечення щонайкращого (оптимального) оброблення необхідні оптимальний фільтр та ідеальний детектор.
14.5. ПОТЕНЦІЙНА ЗАВАДОСТІЙКІСТЬ ПРИЙМАННЯ НЕПЕРЕРВНИХ СИГНАЛІВ
Мінімально можливе значення середньоквадратичного відхилення (похибки)  за заданих умов передавання (задані сигнали, завади, модель каналу зв'язку) визначає потенційну завадостійкість приймання неперервних сигналів. Вона дає максимально можливу точність відновлення первинного сигналу
за заданих умов передавання (задані сигнали, завади, модель каналу зв'язку) визначає потенційну завадостійкість приймання неперервних сигналів. Вона дає максимально можливу точність відновлення первинного сигналу  . Оскільки фізично
. Оскільки фізично  означає потужність завади (див. § 14.1), розрахунок потенційної завадостійкості зводиться до обчислення мінімально можливої потужності завади на виході демодулятора.
означає потужність завади (див. § 14.1), розрахунок потенційної завадостійкості зводиться до обчислення мінімально можливої потужності завади на виході демодулятора.
Але абсолютне значення потужності завади не може бути об'єктивною характеристикою її впливу на сигнал, через те що необхідно враховувати також і рівень завади. Тому для визначення завадостійкості приймання неперервних сигналів обчислюється відношення середніх потужностей сигналу  і завади
і завади  на виході демодулятора:
на виході демодулятора: 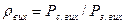 .
.
Виграш демодулятора. У будь-якому демодуляторі відношення сигнал-завада на виході  залежить не тільки від якісних показників демодулятора, але й від відношення сигнал-завада на його вході
залежить не тільки від якісних показників демодулятора, але й від відношення сигнал-завада на його вході 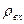 . Через те що існує така об'єктивна закономірність: чим менше завад на вході, тим менше завад на виході, у загальному випадку завадостійкість систем передавання неперервних сигналів зручніше оцінювати виграшем демодулятора у відношенні сигнал-завада:
. Через те що існує така об'єктивна закономірність: чим менше завад на вході, тим менше завад на виході, у загальному випадку завадостійкість систем передавання неперервних сигналів зручніше оцінювати виграшем демодулятора у відношенні сигнал-завада:
 , (16.9)
, (16.9)
при цьому середні потужності завади на вході 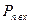 та виході
та виході  демодулятора обчислюються у смузі частот відповідних сигналів.
демодулятора обчислюються у смузі частот відповідних сигналів.
Виграш 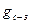 показує зміни відношення сигнал-завада демодулятором. Якщо
показує зміни відношення сигнал-завада демодулятором. Якщо 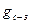 , демодулятор покращує відношення сигнал-завада. Якщо
, демодулятор покращує відношення сигнал-завада. Якщо 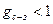 , дістаємо, власне, не виграш, а програш.
, дістаємо, власне, не виграш, а програш.
Розрахункові формули виграшу оптимального демодулятора для різних способів модуляції при завадах у вигляді адитивного білого гауссового шуму подані в табл. 16.3.
Date: 2016-02-19; view: 831; Нарушение авторских прав