Примеры. Задача № 1. Расчет балки – стенки

Задача № 1. Расчет балки – стенки.

Для балки прямоугольного сечения длиной p,высотой h и толщиной 1 (рисунок 16) задана функция напряжений φ(x,y) = а (x ⁴ - 3 x ² y ²) + bху ² и размеры l = 4 м и h = 2 м. Объемными силами следует пренебречь. Коэффициенты а = 1 МН/м⁴, b = 1 МН/м³. Требуется:

1) проверить, можно ли использовать предложенную функцию в качестве решения плоской задачи теории упругости;

2) получить выражения для напряжений;

3) используя граничные условия, записать выражения для внешних усилий, действующих по граням заданной области;

4) по полученным значениям построить эпюры нормальных и сдвигающих усилий;

5) сделать проверку построенных эпюр;

6) в точке «А» с координатами х = 3 м и у = 0,5 м вычислить напряжения , главные напряжения 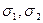и положение главных площадок. Найти τ_мах.

1 Предложенный полином φ(x,y) 4-й степени и его необходимо проверить на соответствие бигармоническому уравнению (7). Для этого берем частные производные от φ(x,y) по х и у вплоть до четвертых производных.

,

,

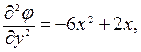
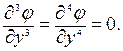
Подставим четвертые производные в уравнение (7):

24 + 2∙(-12) + 0 = 0.

Вывод – предложенную функцию можно использовать в качестве решения плоской задачи.

2 Используя формулы Эри (6) записываем выражения для напряжений:

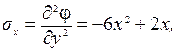
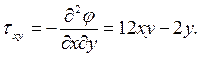
3 Записываем выражения для внешних усилий, действующих по граням заданной области, используя условия на поверхности (5). Для этого проводим внешние (направленные наружу) нормали к граням области и определяем значения направляющих косинусов l и m (рисунок 17).

Правая грань. Ее координаты х = 4 м, - 1 ≤ у ≤ 1 м.

При у = - 1м при у = 1м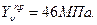

Верхняя грань. Ее координаты: 0 ≤ х ≤ 4 м, у = 1 м.

При х = 0 при х = 4м

, (Квадратная парабола).

При х = 0 при х = 2м при х = 4м

Левая грань. Ее координаты х = 0, - 1 ≤ у ≤ 1 м.

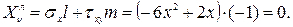
При у = - 1м при у = 1м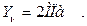

Нижняя грань. Ее координаты: 0 ≤ х ≤ 4 м, у = - 1 м.

При х = 0 при х = 4м

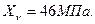
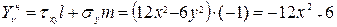, (Квадратная парабола).

При х = 0 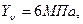при х = 2м при х = 4м

4 Строим эпюры нормальных и сдвигающих усилий.

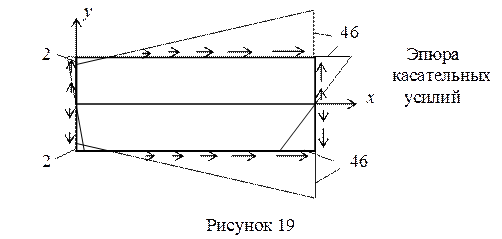
5 Делаем проверку построенных эпюр.

Во первых отметим, что на эпюре касательных усилий выполняется правило парности касательных напряжений в углах прямоугольной области.

Составляем уравнения равновесия для нагрузок, действующих на область.

S х = 0;

S y = 0;

Уравнения равновесия выполняются.

6 Анализируем напряженное состояние в точке А.

,

.

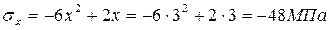Вычисляем главные напряжения.

=29,25 ± 79,1,

s₁ = 108.3 МПа, s₂ = - 49,85 МПа.

Находим положение главных площадок.

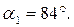
Напряженное состояние в точке А с учетом знаков напряжений показано на рисунок 20.

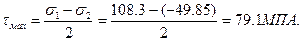
Date: 2016-02-19; view: 1718; Нарушение авторских прав