Показатели финансового состояния 4 page

При трастовом способе предприятие на основе договора доверительного управления имуществом (траста) передает функции управления портфелем банку или другому юридическому лицу, занимающемуся подобной деятельностью.

Работа по формированию и управлению портфелем ценных бумаг складывается из ряда последовательных этапов:

1) выработка инвестиционной политики, определение инвестиционных целей предприятия-инвестора и соотношений доходности и риска;

2) осуществление финансового анализа, изучение отдельных видов и групп ценных бумаг с целью выявления случаев их недооценки рынком;

3) формирование портфеля, определение конкретных бумаг для инвестирования и размера вкладываемых средств;

4) пересмотр портфеля, выявление бумаг, которые необходимо продать или купить;

5) оценка эффективности портфеля, расчет показателей риска и доходности, их сравнение с показателями эталонного портфеля.

Для выработки инвестиционной политики главным является определение инвестиционной цели инвестора. Согласно современной теории портфеля цели инвестора проявляются в его отношении к риску и ожидаемой доходности. Одним из широко применяемых методов определения таких целей является построение кривой безразличия, характеризующей предпочтения инвестора. Это кривая на критериальной плоскости, состоящая из оценок эквивалентных портфелей. Выбор между портфелями, оценки которых лежат на такой кривой, безразличен для инвестора. Вместе с тем сравнение портфелей, оценки которых лежат на разных кривых, свидетельствуют, что любой портфель с оценкой на одной кривой предпочтительнее портфеля с оценкой на другой кривой.

Кривая безразличия может быть представлена как двухмерный график, в котором по оси абсцисс откладывается риск, мерой которого является стандартное отклонение (σ_р), а по оси ординат — вознаграждение за риск, мерой которого

является ожидаемая доходность ().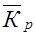

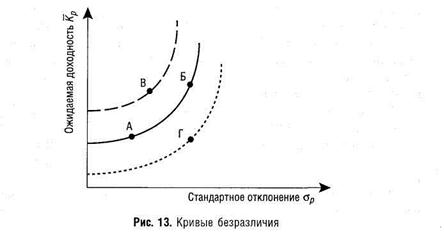
На рисунке 13 представлены три кривые безразличия, каждая из которых представляет собой все возможные комбинации оценок инвестора в отношении риска и доходности портфелей.

Кривые безразличия имеют два важных свойства. Первое: все портфели, лежащие на одной кривой безразличия, являются равноценными. Портфели А и Б будут равноценными для инвестора, несмотря на то что они имеют различные ожидаемые доходности и стандартные отклонения. При этом портфель Б имеет больший риск, чем портфель А, и с точки зрения этого параметра он хуже, зато портфель Б выигрывает за счет более высокой ожидаемой доходности, чем у портфеля А.

Второе свойство кривых безразличия: любой портфель, лежащий на кривой, расположенной выше и левее, более привлекателен для инвестора по сравнению с портфелем, лежащим на кривой, расположенной ниже и правее. Портфель В, который лежит на кривой, находящейся выше и левее кривой портфеля А, имеет большую доходность, что компенсирует его больший риск, но в то же время меньший риск, чем портфель Б, что компенсирует меньшую ожидаемую доходность, поэтому портфель В предпочтительнее для инвестора по сравнению с портфелями А и Б.

В силу описанных свойств кривые безразличия никогда не пересекаются.

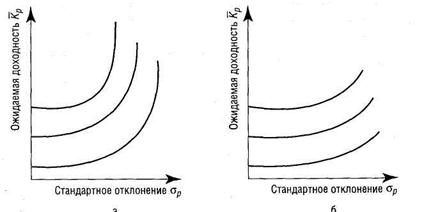
Исходя из отношения инвестора к риску и доходности и их оценок инвестор может иметь бесконечное число кривых безразличия. Эти кривые проходят через каждую точку критериальной плоскости, целиком заполняя ее. Характер расположения кривых означает индивидуальную для инвестора взаимозаменяемость доходности и риска. Крутые кривые безразличия означают более осторожного инвестора, чем пологие кривые (рис. 14).

Рис. 14 Виды кривых безразличия а – крутые кривые, б – пологие кривые

В первом случае (а) инвестор готов допустить малое увеличение риска лишь с компенсацией в виде значительного увеличения доходности. Во втором случае (б) инвестор ради небольшого увеличения доходности готов принять значительное увеличение риска.

Таким образом, менеджер в работе по формированию и управлению портфелем должен определить ожидаемую доходность и риск для каждого потенциального портфеля, построить график и выбрать один портфель, который лежит на кривой безразличия выше и левее относительно других кривых.

При выборе портфеля на базе кривых безразличия менеджер исходит из двух предположений: о ненасыщаемости и об избежании риска. Предполагается, что инвестор всегда предпочитает увеличение уровня своего благосостояния. Инвестор, делающий выбор между двумя одинаковыми во всем (кроме ожидаемой доходности) портфелями, выберет портфель с большей доходностью. Однако если инвестору нужно выбрать между портфелями с одинаковым уровнем ожидаемой доходности, но разным уровнем риска, то он выберет портфель с меньшим риском.

Итак, главными параметрами при управлении портфелем, которые необходимо определить менеджеру, являются ожидаемая доходность и риск. Формируя портфель, менеджер не может точно определить будущую динамику его доходности и риска, поэтому свой выбор он строит на ожидаемых значениях. Данные величины оцениваются на основе статистических отчетов за предыдущие периоды времени. Полученные оценки менеджер может корректировать согласно своим представлениям о развитии будущей конъюнктуры.

Поскольку портфель, формируемый инвестором, состоит из набора различных ценных бумаг, его доходность и риск будут зависеть от доходности и риска каждой отдельной ценной бумаги. Кроме того, ожидаемая доходность портфеля зависит от размера начального капитала, инвестированного в конкретные ценные бумаги.

Ожидаемая доходность портфеля может быть вычислена двумя способами. Первый способ основан на использовании стоимостей на конец периода и заключается в вычислении ожидаемой цены портфеля в конце периода и уровня его доходности:

_

K_p=(W₁ –W₀):W₀, (122)

где К_р — ожидаемая доходность портфеля;

W₀ — начальная стоимость портфеля;

W₁ — ожидаемая стоимость портфеля в конце периода.

Второй способ построен на использовании ожидаемой доходности ценных бумаг и включает вычисление ожидаемой доходности портфеля как средневзвешенной ожидаемых доходностей ценных бумаг, входящих в портфель. Относительные рыночные курсы ценных бумаг портфеля используются в качестве весов:

__ N

K_p = ∑x_i x k_i = x_i x k_i + x₂ x k₂ + …+ x_N x k_N, (123)

i=1

где x_i — доля начальной стоимости портфеля, инвестированная в ценную бумагу;

k_i — ожидаемая доходность ценной бумаги;

N — количество ценных бумаг в портфеле.

Инвестор, который желает получить наибольшую возможную доходность, должен иметь портфель, состоящий из одной ценной бумаги, у которой ожидаемая доходность наибольшая. Однако менеджер посоветует инвестору диверсифицировать свой портфель, т.е. включить в него несколько ценных бумаг, снижая тем самым риск.

Инвестиционный риск портфеля определяется как изменчивость доходности, которая измеряется стандартным отклонением (дисперсией) распределения доходности портфеля.

Ожидаемый риск портфеля представляет собой сочетание стандартных отклонений (дисперсий) входящих в него ценных бумаг. Однако в отличие от ожидаемой доходности риск портфеля не является обязательно средневзвешенной величиной стандартных отклонений (дисперсий) доходности ценных бумаг. Дело в том, что различные ценные бумаги могут по-разному реагировать на изменение конъюнктуры рынка. В результате стандартные отклонения (дисперсии) доходности различных ценных бумаг в ряде случаев будут гасить друг друга, что приведет к снижению риска портфеля. Риск портфеля зависит от того, в каком направлении и в какой степени меняются доходности входящих в него ценных бумаг при изменении конъюнктуры рынка.

Для определения взаимосвязи и направления изменения доходностей ценных бумаг используют показатель ковариации и коэффициент корреляции.

Показатель ковариации определяется по формуле

n _

COV _XY = [ ∑ (k_X - k_X) X (k_Y – k_Y)]: n, (124)

i=1

где COV _XY – ковариация доходности ценных бумаг;

k_X,_y – норма дохода по ценной бумаге;

_

k_X,_y – ожидаемая норма дохода по ценной бумаге;

n – число наблюдений за доходностью ценных бумаг.

Положительное значение ковариации свидетельствует, что доходность ценных бумаг изменяется в одном направлении, отрицательное — что в обратном. Нулевое значение ковариации означает, что взаимосвязь между доходностями активов отсутствует.

Другим показателем взаимосвязи изменения доходностей цен­ных бумаг служит коэффициент корреляции (r_xy):

r_xy = COV_xy: (σ_x х σ_y), (125)

где σ_ху — стандартное отклонение доходности ценной бумаги.

Коэффициент корреляции меняется в пределах от —1 до +1. Положительное значение коэффициента говорит о том, что доходности ценных бумаг меняются в одном направлении с изменением конъюнктуры, отрицательное — что в противоположном. При нулевом значении коэффициента корреляции связь между доходностями ценных бумаг отсутствует.

Риск портфеля, состоящего из двух ценных бумаг, рассчитывает­ся по формуле

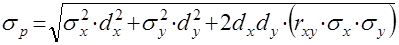, (126)

где σ_р – стандартное отклонение по портфелю;

σ_{х, y} – стандартное отклонение по ценной бумаге;

d_х, _y – доля ценной бумаги в портфеле;

r_ху – коэффициент корреляции между ценными бумагами х и у.

Риск портфеля, объединяющего большее число ценных бумаг, требует построения ковариационной матрицы с данными о дисперсии и ковариации бумаг, а также ее решения.

Финансовый анализ проводится на втором этапе процесса управления портфелем ценных бумаг и представляет собой подготовку данных, необходимых для работы менеджера по управлению портфелем.

Проведение финансового анализа связано с необходимостью определения конкретных характеристик ценных бумаг и выявления тех ценных бумаг, которые представляются инвесторам неверно оце­ненными в настоящем.

При определении основных характеристик рассматриваются главные факторы, влияющие на ценные бумаги, и устанавливается их подверженность этому влиянию. Таким фактором может быть, например, размер налоговых выплат, который не одинаков для ценных бумаг, представляющих интерес для инвестора.

Существенное влияние на принятие инвестиционных решений оказывает уровень инфляции, с увеличением периода которой доход по акциям меняется. Менеджер должен также учитывать взаимосвязь прибыли, дивидендов и инвестиций. При принятом варианте распределения прибыли из нее финансируются новые инвестиции и выплачиваются дивиденды акционерам. Выплата более высоких дивидендов и увеличение размера инвестиций требуют получения дополнительных средств извне, что достигается, в частности, за счет новой продажи акций. Поэтому необходимо проанализировать дивидендную политику предприятия, вероятный приток средств инвесторов в будущем. На основе анализа оценивают ставку дивидендной доходности ценной бумаги в перспективе (например, в следующем году) и определяют вероятность ее включения в портфель. Также необходимо установить возможный риск по данной ценной бумаге, чтобы не подвергать риску весь портфель.

Выявление неверно оцененных ценных бумаг обычно проводится с помощью методов фундаментального анализа и включает поиск и обнаружение таких ситуаций, когда оценки будущих доходов и дивидендов предприятия либо существенно отличаются от общепринятого мнения, либо являются более точными, либо еще не получили отражения в рыночном курсе ценных бумаг.

В рамках фундаментального анализа выявление неверно оцененных ценных бумаг может осуществляться на основе определения их внутренней (истинной) стоимости.

Считается, что внутренняя (истинная) стоимость любого актива равна приведенной стоимости всех наличных денежных потоков, которые владелец актива рассчитывает получить в будущем. Поэтому менеджер стремится определить время поступления и величину наличных денежных потоков, затем рассчитывает их приведенную стоимость, используя ставку дисконтирования, и составляет прогноз величины дивидендов и доходов, которые будут получены в дальнейшем.

Процедура анализа внутренней стоимости аналогична методу чистой приведенной стоимости и базируется на оценке капитализации дохода. Если применить метод капитализации дохода к оценке облигаций, то суть его будет состоять в сравнении двух значений показателя доходности к погашению: существующей доходности и требуемой (т.е. того значения, которое является, по мнению менеджера, правильным). Внутренняя стоимость облигации (V) может быть вычислена по формуле

n

V = ∑С_t : (1+y^*)^t, (127)

t=1

Где С_t – предполагаемый денежный поток (выплаты инвестору) по годам;
y^* - требуемая доходность к погашению;

n- остаточный срок обращения.

Так как цена покупки облигации — это ее рыночный курс (Р), то для менеджера чистая приведенная стоимость (NPV) равняется разности между стоимостью облигации (V) и ценой покупки:

n

NPV = V – P = [∑С_t: (1+y^*)^t] – P. (128)

t=1

Если облигация имеет положительное значение NPV, она является недооцененной. Отрицательное значение NPV свидетельствует о переоцененности облигации. Наконец, значение NPV, равное нулю, рассматривается как точная оценка облигации.

Метод капитализации дохода можно применить и к оценке акций. Внутренняя (истинная) стоимость капитала (К) будет рассчитываться как сумма приведенных стоимостей ожидаемых поступлений и выплат:

∞

V = ∑ С_t:(1 + k)^t, (129)

t=1

где С_t - ожидаемое поступление (или выплата), связанное с капиталом в момент времени t;

k - ставка дисконтирования для денежных потоков данной степени риска.

Так как денежный поток ожидается в будущем, то его величина корректируется с помощью ставки дисконтирования, учитывающей не только изменение стоимости денег во времени, но и фактор риска.

В приведенном равенстве ставка дисконтирования предполагается постоянной в течение всего времени инвестирования (до бесконечности).

Для удобства расчетов текущий момент времени принимается равным нулю. Если затраты на приобретение актива в момент времени t = О составляют Р, то его чистая приведенная стоимость (NPV) равна разности между внутренней стоимостью актива и затратами на приобретение:

∞

NPV = V – P = [∑С_t: (1+k)^t] – P. (130)

t=1

Расчет NPV дает возможность принимать решение о приобретении актива (акции). Акция рассматривается как приемлемая и считается недооцененной, если ее NPV > 0. Акция рассматривается как неприемлемая и считается переоцененной, если ее NPV < 0.

Акция является недооцененной, если V > Р, и переоцененной, если V< Р.

Так как финансовые поступления, связанные с инвестициями в обыкновенные акции,— это дивиденды, которые владелец акций ожидает получить в будущем, то способ оценки акций по методу капитализации дохода называют моделью дисконтирования дивидендов. Для определения внутренней стоимости акций (V) используют равенство:

∞

V = ∑ D_t:(1 + k)^t, (131)

t=1

где D_t — ожидаемые выплаты по акции в период времени t.

Дополнительные трудности в расчетах возникают в связи с необходимостью прогнозирования бесконечного потока платежей по дивидендным выплатам, так как время обращения обыкновенных акций не ограничено. Решить данную проблему и сделать расчеты можно с учетом некоторых предположений относительно роста дивидендов в будущем.

Первое предположение заключается в том, что размер дивидендов остается неизменным. Это простейший случай, когда темп роста дивидендов равен нулю, — модель нулевого роста. Внутренняя стоимость акции (V) в этом случае определяется по формуле

V=D₀:k, (132)

где D₀ — фиксированные дивиденды.

Модель с нулевым ростом применяется также для определения внутренней стоимости привилегированных акций, так как по большинству привилегированных акций, так как по большинству привилегированных акций регулярно выплачиваются дивиденды фиксированного размера.

Второе предположение связано с изменяющимися дивидендами, которые растут от периода к периоду в одной пропорции, т.е. с одинаковым темпом роста. Модель постоянного роста предполагает, что дивиденды на одну акцию, выплаченные за предыдущий год (Do), вырастут в данной пропорции (g) так, что в следующем году ожидаются выплаты в размере: D1 = Do(1 + g), через год — в размере: D2 = D 1 (1 + g), и т.д.

Тогда внутренняя стоимость акции будет равна:

∞

V = ∑ D₀ (1+g)^t : (1+k)^t. (133)

t=1

Третье предположение описывается с помощью модели переменного роста. Главная особенность этой модели — период времени в будущем (Т), после которого ожидается, что дивиденды будут расти с постоянным темпом (g). При этом необходимо составить прогноз дивидендов до периода Т исходя из индивидуального прогноза по величине дивидендов для каждого подпериода, а также рассчитать наступление момента Т. После наступления момента Т дивиденды будут расти следующим образом:

D _{T+1 =} D_t (1+g);

D _{T+2 =} D _T+1 + 1 (1+g) = D_T (1+g)²;

D _{T+3 =} D _T+2 + 1 (1+g) = D_T (1+g)³ и т.д.

Внутренняя стоимость акции в этой модели будет определяться как сумма приведенной стоимости дивидендов, выплачиваемых до периода Т ₁ включительно, и приведенной стоимости всех выплат дивидендов после периода Т₂:

V = V_T1 + V_T2 (134)

Формула расчета внутренней стоимости акций (V) примет следующий вид:

Т

V = ∑D_t: (1+k)^t + D_T+1: [(k- g)(1+k)^T]. (135)

t=1

Определенная таким образом внутренняя стоимость акций (V) сравнивается с ее текущим рыночным курсом (Р). Если акция недооценена, то ее внутренняя стоимость выше текущего курса (V > P), и такие акции рекомендуют покупать. В случае превышения текущего курса над внутренней стоимостью (V < P) акция считается переоцененной, что служит сигналом к ее продаже.

При пассивном управлении портфелем менеджер выбирает в качестве цели некий индекс и формирует портфель, изменение доходности которого соответствует динамике данного индекса. Пассивное управление отсюда получило название индексирования, а пассивные портфели — индексных фондов.

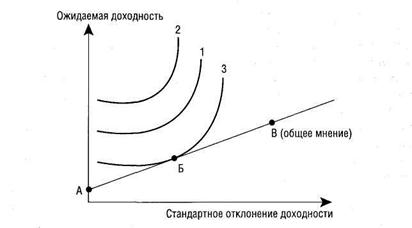
Графически пример пассивного управления портфелем менеджером представлен на рис. 15.

рис.15 Кривые безразличия (1, 2, 3) при пассивном управлении портфелем

Менеджер формирует портфель, в котором сочетание безрисковых ценных бумаг и индексного фонда схоже с рыночным портфелем. Точка А показывает доходность с нулевым риском, которую обеспечивают безрисковые ценные бумаги. Точка В — риск и ожидаемую доходность среднерыночного портфеля, которые соответствуют общему мнению на рынке. Линия, идущая через точки А и В, представляет собой сочетание двух типов инвестиций. Кривые безразличия (1, 2, 3) показывают отношение инвестора, для которого менеджер формирует портфель, к риску и доходности. Точка Б, в которой кривая безразличия является касательной к линии АВ, представляет собой оптимальное сочетание доходности и риска.

Обычно при пассивном управлении менеджер вносит изменения в портфель, если меняются предпочтения инвестора, значение безрисковой ставки либо общие прогнозы риска и доходности рыночного портфеля. Поэтому задача менеджера по управлению портфелем заключается в наблюдении за значениями безрисковой ставки и состоянием индексного фонда, а также постоянном контакте с инвестором.

Практика показывает, что только 4% западных менеджеров используют пассивную тактику.

Активные менеджеры имеют собственные прогнозы риска и ожидаемой доходности, которые отличаются от общего мнения рынка. Они считают, что время от времени появляются неверно оцененные рынком ценные бумаги. При этом одни менеджеры могут быть настроены как «быки» по сравнению с общим мнением рынка относительно той или иной бумаги, другие — как «медведи». Первые будут держать в портфеле ценные бумаги в пропорции, большей чем нормальная, а вторые — в меньшей чем нормальная.

Основой активного управления портфелем является выбор ценных бумаг, приемлемых для формирования портфеля.

Выбор ценных бумаг может осуществляться несколькими способами. Перед активным менеджером стоит задача прогнозирования ожидаемой доходности, стандартного отклонения и ковариации всех доступных ценных бумаг. На основе этих прогнозов определяется эффективное множество, для которого будут построены кривые безразличия. Понятие эффективного множества связано со множеством всех оценок допустимых портфелей (речь идет о множестве оценок, а не портфелей), которое геометрически изображается множеством точек на критериальной плоскости. Поскольку инвестор при выборе ценных бумаг исходит лишь из оценок их доходности и риска, то множество показывает пределы эффективности его выбора.

Если объединить в портфель несколько ценных бумаг, корреляция доходности которых лежит в диапазоне от —1 до +1, то в зависимости от их удельных весов можно построить множество портфелей с различными параметрами риска и доходности, которые расположатся в рамках фигуры АБВГ на рис. 16.

Рациональный инвестор будет стремиться минимизировать свой риск и увеличить доходность, поэтому всем возможным портфелям, представленным на рис. 16, он предпочтет только те, которые расположены на отрезке ДЕ и составляют эффективную границу множества. Это объясняется тем, что портфели на кривой ДЕ являются доминирующими по отношению к портфелям с тем же уровнем риска или с той же доходностью. Доминирующий портфель — это портфель, который имеет самый высокий уровень доходности для данного уровня риска или наименьшее значение риска для данного значения доходности. Доминирующий портфель является лучшим выбором для инвестора из числа всех возможных портфелей.

Ожидаемая доходность

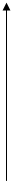
Стандартное отклонение доходности

Рис. 16. Кривые безразличия при активном управлении портфелем

Набор портфелей на отрезке ДЕ называют эффективным набором, состоящим из доминирующих портфелей. Эффективный набор портфелей на кривой ДЕ составляет эффективную границу, определить которую можно с помощью компьютерных программ, рассчитав соответствующие удельные веса входящих в портфель ценных бумаг, при которых минимизируется значение стандартного отклонения для каждого данного уровня доходности.

Менеджеру следует делать инвестиции в те ценные бумаги, которые формируют оптимальный портфель инвестора, соответствующий точке, в которой кривая безразличия является касательной к эффективному множеству (точка Ж).

Однако обычно используется двухэтапная процедура выбора ценных бумаг и размещения активов. Сначала менеджер принимает решение инвестировать средства в обыкновенные акции и корпоративные облигации. Далее определяются показатели ожидаемой доходности, стандартного отклонения и ковариации для всех рассматриваемых акций, формируется эффективное множество и оптимальный портфель акций (аналогичная процедура проводится и в отношении облигаций). На втором этапе происходит размещение активов, когда средства инвестора делятся между портфелями акций и облигаций. Снова составляются прогнозы ожидаемой доходности и стандартного отклонения для оптимальных портфелей акций и облигаций, а также степени ковариации между ними, рассчитываются показатели стандартного отклонения и ожидаемой доходности при всех возможных сочетаниях бумаг двух портфелей. После выбора эффективного множества данных сочетаний можно использовать кривые безразли­чия инвестора для выбора оптимального портфеля.

По истечении определенного времени первоначально сформированный портфель уже не может рассматриваться менеджером в качестве оптимального, наилучшего для инвестора в связи с изменением его отношения к риску и доходности, а также инвестиционных предпочтений или изменением прогнозов самого менеджера. В этом случае менеджер должен пересмотреть портфель. Во-первых, он должен определить, каким будет новый оптимальный портфель; во-вторых, выявить те виды бумаг в существующем портфеле, которые необходимо продать, и виды бумаг, которые следует купить взамен; в-третьих, переструктурировать имеющийся портфель.

Пересмотр портфеля связан с определенными дополнительными расходами, например, на комиссионные брокерам, потери от изменения цен на бумаги, разницу между ценами покупки и продажи и т.д. Для того чтобы пересмотр был эффективным, выгоды от пересмотра портфеля должны превышать издержки, обеспечивать увеличение ожидаемой доходности, а также уменьшение стандартного отклонения портфеля.

Основная цель менеджера состоит в том, чтобы подобрать такие бумаги, которые с учетом дополнительных издержек, связанных с пересмотром, позволят максимально улучшить показатели риска и доходности портфеля. Для снижения издержек многие менеджеры прибегают к стратегии пересмотра не в отношении отдельных бумаг, а целых классов активов, используя рынок свопов.

Свопы в чистом виде представляют собой контракты между двумя сторонами, которые обмениваются денежными потоками в течение определенного периода времени. Рынок свопов не регулируется со стороны государства. Динамичность, появление новых типов и видов свопов и отсутствие гарантий надежности партнеров являются его основными характеристиками. Участвующие в свопе лица сами несут риск надежности партнера и поэтому должны обращать особое внимание на его кредитоспособность, чтобы уменьшить риск неплатежа по контракту. Нередко дилером по свопам выступает банк, который организует свопы для своих клиентов, выступая стороной контракта.

Наиболее распространенными являются свопы на акции и на процентную ставку.

В свопе на акции одна сторона соглашается уплатить другой сумму средств, величина которой зависит от изменения согласованного фондового индекса. Вторая сторона в свою очередь соглашается уплатить первой фиксированную сумму средств исходя из текущей процентной ставки. Оба потока платежей согласно контракту должны быть осуществлены в течение конкретного периода и предполагают выплату определенной ставки процента от номинала, указанного в контракте (ставка процента является плавающей для одной сто­роны и фиксированной для другой). По сути, с помощью свопа первая сторона продает акции и покупает облигации, а вторая сторона — продает облигации и покупает акции. Обе стороны эффективно пересматривают свои портфели с минимальными дополнительными издержками, которые определяются только размером комиссионных, уплачиваемых банку за организацию свопа.

В свопе на процентную ставку одна сторона соглашается осуществить в пользу другой стороны поток платежей, величина которого устанавливается на основе представительной процентной ставки (популярной является лондонская ставка предложения по межбанковским депозитам — LIBOR). Вторая сторона соглашается осуществить в пользу первой стороны поток фиксированных платежей, который основан на уровне процентных ставок в момент подписания контракта. Оба потока платежей должны быть осуществлены в течение конкретного периода и определяются в виде процентов от номинала контракта. Для одной стороны процент носит плавающий характер, для другой стороны — фиксированный. С помощью свопа на ставку процента первая сторона, по существу, продает краткосрочные бумаги с фиксированным доходом и покупает долгосрочные облигации, а вторая сторона продает долгосрочные облигации и покупает краткосрочные бумаги с фиксированным доходом. В результате обе стороны эффективно и с минимальными дополнительными издержками пересматривают свои портфели.

Date: 2015-04-23; view: 678; Нарушение авторских прав